
”¾ĢāÄæ”æijøß¼¶ÖŠŃ§ŌŚ½ńÄź”°ĪåŅ»”±ĘŚ¼äøųŠ£ÄŚĖłÓŠ½ĢŹŅ°²×°ĮĖĶ¬Ņ»ŠĶŗŵÄæÕµ÷£¬¹ŲÓŚÕāÅśæÕµ÷µÄŹ¹ÓĆÄźĻŽ![]() µ„Ī»£ŗÄź
µ„Ī»£ŗÄź![]() ŗĶĖłÖ§³öµÄĪ¬»¤·ŃÓĆ
ŗĶĖłÖ§³öµÄĪ¬»¤·ŃÓĆ![]() µ„Ī»£ŗĒ§ŌŖ
µ„Ī»£ŗĒ§ŌŖ![]() ³§¼ŅĢį¹©µÄĶ³¼Ę׏ĮĻČē±ķ£ŗ
³§¼ŅĢį¹©µÄĶ³¼Ę׏ĮĻČē±ķ£ŗ
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
![]() ČōxÓėyÖ®¼äŹĒĻߊŌĻą¹Ų¹ŲĻµ£¬ĒėĒó³öĪ¬»¤·ŃÓĆy¹ŲÓŚxµÄĻߊŌ»Ų¹éÖ±Ļß·½³Ģ
ČōxÓėyÖ®¼äŹĒĻߊŌĻą¹Ų¹ŲĻµ£¬ĒėĒó³öĪ¬»¤·ŃÓĆy¹ŲÓŚxµÄĻߊŌ»Ų¹éÖ±Ļß·½³Ģ![]() £»
£»
![]() Čō¹ę¶Øµ±Ī¬»¤·ŃÓĆy³¬¹ż
Čō¹ę¶Øµ±Ī¬»¤·ŃÓĆy³¬¹ż![]() Ē§ŌŖŹ±£¬øĆÅśæÕµ÷±ŲŠė±Ø¶Č£¬ŹŌøł¾Ż
Ē§ŌŖŹ±£¬øĆÅśæÕµ÷±ŲŠė±Ø¶Č£¬ŹŌøł¾Ż![]() µÄ½įĀŪĒóøĆÅśæÕµ÷Ź¹ÓĆÄźĻŽµÄ×ī“óÖµ
µÄ½įĀŪĒóøĆÅśæÕµ÷Ź¹ÓĆÄźĻŽµÄ×ī“óÖµ![]() ½į¹ūČ”ÕūŹż
½į¹ūČ”ÕūŹż![]() ²Īæ¼¹«Ź½£ŗ
²Īæ¼¹«Ź½£ŗ![]() £¬
£¬![]() £®
£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©10
£»£Ø2£©10
”¾½āĪö”æ
![]() ÓÉĢāŅāŹ×ĻČĒóµĆŃł±¾ÖŠŠÄµć£¬Č»ŗóĒó½ā»Ų¹é·½³Ģ¼“æÉ£»
ÓÉĢāŅāŹ×ĻČĒóµĆŃł±¾ÖŠŠÄµć£¬Č»ŗóĒó½ā»Ų¹é·½³Ģ¼“æÉ£»![]() ĄūÓĆ
ĄūÓĆ![]() µÄ½įĀŪ½įŗĻĢāŅāµĆµ½²»µČŹ½£¬Ēó½ā²»µČŹ½¼“æÉĒóµĆ×īÖÕ½į¹ū
µÄ½įĀŪ½įŗĻĢāŅāµĆµ½²»µČŹ½£¬Ēó½ā²»µČŹ½¼“æÉĒóµĆ×īÖÕ½į¹ū
![]() ÓÉĢāŅāæÉµĆ£ŗ
ÓÉĢāŅāæÉµĆ£ŗ![]() £¬
£¬![]() £¬
£¬
Ōņ£ŗ![]() £¬
£¬
![]() £¬
£¬
»Ų¹é·½³ĢĪŖ£ŗ![]() £¬
£¬
![]() µ±Ī¬»¤·ŃÓĆy³¬¹ż
µ±Ī¬»¤·ŃÓĆy³¬¹ż![]() ĶņŌŖŹ±£¬
ĶņŌŖŹ±£¬
¼“£ŗ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬
Ōņ“ÓµŚ11ÄźæŖŹ¼ÕāÅśæÕµ÷±ŲŠė±Ø·Ļ£¬øĆÅśæÕµ÷Ź¹ÓĆÄźĻŽµÄ×ī“óÖµĪŖ10Äź£®
“š£ŗøĆÅśæÕµ÷Ź¹ÓĆÄźĻŽµÄ×ī“óÖµĪŖ10Äź


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢĘ·ŌŚ½ü30ĢģÄŚĆ漞µÄĻśŹŪ¼Ūøń![]() £Øµ„Ī»£ŗŌŖ£©ÓėĻśŹŪŹ±¼ä
£Øµ„Ī»£ŗŌŖ£©ÓėĻśŹŪŹ±¼ä![]() £Øµ„Ī»£ŗĢģ£©µÄŗÆŹż¹ŲĻµĪŖ
£Øµ„Ī»£ŗĢģ£©µÄŗÆŹż¹ŲĻµĪŖ![]() £¬
£¬![]() £¬ĒŅøĆÉĢĘ·µÄČÕĻśŹŪĮæQ£Øµ„Ī»:¼ž£©ÓėĻśŹŪŹ±¼ä
£¬ĒŅøĆÉĢĘ·µÄČÕĻśŹŪĮæQ£Øµ„Ī»:¼ž£©ÓėĻśŹŪŹ±¼ä![]() £Øµ„Ī»£ŗĢģ£©µÄŗÆŹż¹ŲĻµĪŖ
£Øµ„Ī»£ŗĢģ£©µÄŗÆŹż¹ŲĻµĪŖ![]() £¬ŌņÕāÖÖÉĢĘ·µÄČÕĻśŹŪĮ潚¶ī×ī“óµÄŅ»ĢģŹĒ30ĢģÖŠµÄµŚ__________Ģģ£®
£¬ŌņÕāÖÖÉĢĘ·µÄČÕĻśŹŪĮ潚¶ī×ī“óµÄŅ»ĢģŹĒ30ĢģÖŠµÄµŚ__________Ģģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¹żµć![]() µÄÖ±Ļß
µÄÖ±Ļß![]() µÄ²ĪŹż·½³ĢĪŖ
µÄ²ĪŹż·½³ĢĪŖ![]() £Ø
£Ø![]() ĪŖ²ĪŹż£¬
ĪŖ²ĪŹż£¬ ![]() ĪŖ
ĪŖ![]() µÄĒ抱½Ē£©.ŅŌ×ų±źŌµćĪŖ¼«µć£¬
µÄĒ抱½Ē£©.ŅŌ×ų±źŌµćĪŖ¼«µć£¬ ![]() ÖįµÄÕż°ėÖįĪŖ¼«Öį£¬½ØĮ¢¼«×ų±źĻµ.ĒśĻß
ÖįµÄÕż°ėÖįĪŖ¼«Öį£¬½ØĮ¢¼«×ų±źĻµ.ĒśĻß![]() £¬ĒśĻß
£¬ĒśĻß![]() .
.
£Ø1£©ČōÖ±ĻßÓė![]() ÓŠĒŅ½öÓŠŅ»øö¹«¹²µć£¬ĒóÖ±Ļß
ÓŠĒŅ½öÓŠŅ»øö¹«¹²µć£¬ĒóÖ±Ļß![]() µÄ¼«×ų±ź·½³Ģ£»
µÄ¼«×ų±ź·½³Ģ£»
£Ø2£©ČōÖ±Ļß![]() ÓėĒśĻß
ÓėĒśĻß![]() ½»ÓŚ²»Ķ¬Į½µć
½»ÓŚ²»Ķ¬Į½µć![]() £¬Óė
£¬Óė![]() ½»ÓŚ²»Ķ¬Į½µć
½»ÓŚ²»Ķ¬Į½µć![]() £¬ÕāĖĵć“Ó×óµ½ÓŅŅĄ“ĪĪŖ
£¬ÕāĖĵć“Ó×óµ½ÓŅŅĄ“ĪĪŖ![]() £¬Ēó
£¬Ēó![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”湩µē²æĆŶŌijÉēĒų1000Ī»¾ÓĆń2017Äź12ŌĀ·ŻČĖ¾łÓƵēĒéæö½ųŠŠĶ³¼Ęŗ󣬰“ČĖ¾łÓƵēĮæ·ÖĪŖ![]() Īå×飬ÕūĄķµĆµ½ČēĻĀµÄʵĀŹ·Ö²¼Ö±·½Ķ¼£¬ŌņĻĀĮŠĖµ·Ø“ķĪóµÄŹĒ£Ø £©
Īå×飬ÕūĄķµĆµ½ČēĻĀµÄʵĀŹ·Ö²¼Ö±·½Ķ¼£¬ŌņĻĀĮŠĖµ·Ø“ķĪóµÄŹĒ£Ø £©
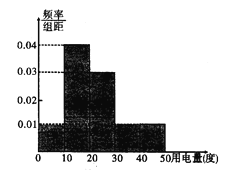
A. 12ŌĀ·ŻČĖ¾łÓƵēĮæČĖŹż×ī¶ąµÄŅ»×éÓŠ400ČĖ
B. 12ŌĀ·ŻČĖ¾łÓƵēĮæ²»µĶÓŚ20¶ČµÄÓŠ500ČĖ
C. 12ŌĀ·ŻČĖ¾łÓƵēĮæĪŖ25¶Č
D. ŌŚÕā1000Ī»¾ÓĆńÖŠČĪŃ”1Ī»ŠÖśŹÕ·Ń£¬Ń”µ½µÄ¾ÓĆńÓƵēĮæŌŚ![]() ”Ŗ×éµÄøÅĀŹĪŖ
”Ŗ×éµÄøÅĀŹĪŖ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčŗÆŹżf£Øx£©=ex+sinx£¬g£Øx£©=ax£¬F£Øx£©=f£Øx£©©g£Øx£©£®
£Ø1£©Čōx=0ŹĒF£Øx£©µÄ¼«Öµµć£¬ĒóaµÄÖµ£»
£Ø2£©µ± a=1Ź±£¬ÉčP£Øx1 £¬ f£Øx1£©£©£¬Q£Øx2 £¬ g£Øx2£©£©£Øx1£¾0£¬x2£¾0£©£¬ĒŅPQ”ĪxÖį£¬ĒóP”¢QĮ½µć¼äµÄ×ī¶Ģ¾ąĄė£»
£Ø3£©Čōx”Ż0Ź±£¬ŗÆŹży=F£Øx£©µÄĶ¼ĻóŗćŌŚy=F£Ø©x£©µÄĶ¼ĻóÉĻ·½£¬Ē󏵏żaµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĖę×Å»„ĮŖĶųµÄ·¢Õ¹£¬ŅʶÆÖ§ø¶![]() ÓÖ³ĘŹÖ»śÖ§ø¶
ÓÖ³ĘŹÖ»śÖ§ø¶![]() Öš½„ÉīČėČĖĆńČŗÖŚµÄÉś»ī
Öš½„ÉīČėČĖĆńČŗÖŚµÄÉś»ī![]() Ä³Ń§Š£ŠĖȤŠ”×éĪŖĮĖĮĖ½āŅʶÆÖ§ø¶ŌŚČĖĆńČŗÖŚÖŠµÄŹģÖŖ¶Č£¬¶Ō
Ä³Ń§Š£ŠĖȤŠ”×éĪŖĮĖĮĖ½āŅʶÆÖ§ø¶ŌŚČĖĆńČŗÖŚÖŠµÄŹģÖŖ¶Č£¬¶Ō![]() ĖźµÄČĖČŗĖ껜³éŃłµ÷²é£¬µ÷²éµÄĪŹĢāŹĒÄć»įŹ¹ÓĆŅʶÆÖ§ø¶Āš£æ”±ĘäÖŠ£¬»Ų“š”°»į”±µÄ¹²ÓŠ50øöČĖ£¬°ŃÕā50øöČĖ°“ÕÕÄźĮä·Ö³É5×飬²¢»ęÖĘ³öʵĀŹ·Ö²¼±ķ
ĖźµÄČĖČŗĖ껜³éŃłµ÷²é£¬µ÷²éµÄĪŹĢāŹĒÄć»įŹ¹ÓĆŅʶÆÖ§ø¶Āš£æ”±ĘäÖŠ£¬»Ų“š”°»į”±µÄ¹²ÓŠ50øöČĖ£¬°ŃÕā50øöČĖ°“ÕÕÄźĮä·Ö³É5×飬²¢»ęÖĘ³öʵĀŹ·Ö²¼±ķ![]() ²æ·ÖŹż¾ŻÄ£ŗż²»Ēå
²æ·ÖŹż¾ŻÄ£ŗż²»Ēå![]() Čē±ķ£ŗ
Čē±ķ£ŗ
·Ö×é | ʵŹż | ʵĀŹ | |
µŚ1×é |
| 10 |
|
µŚ2×é |
|
|
|
µŚ3×é |
| 15 |
|
µŚ4×é |
|
|
|
µŚ5×é |
| 2 |
|
ŗĻ¼Ę | 50 |
| |
![]() ±ķÖŠ
±ķÖŠ![]() “¦µÄŹż¾Ż·Ö±šŹĒ¶ąÉŁ£æ
“¦µÄŹż¾Ż·Ö±šŹĒ¶ąÉŁ£æ
![]() “ÓµŚ1×飬µŚ3×飬µŚ4×éÖŠÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬ĒóĆæ×é³éČ”µÄČĖŹż£®
“ÓµŚ1×飬µŚ3×飬µŚ4×éÖŠÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬ĒóĆæ×é³éČ”µÄČĖŹż£®
![]() ŌŚ
ŌŚ![]() ³éČ”µÄ6ČĖÖŠŌŁĖ껜³éČ”2ČĖ£¬ĒóĖł³éČ”µÄ2ČĖĄ“×ŌĶ¬Ņ»øö×éµÄøÅĀŹ£®
³éČ”µÄ6ČĖÖŠŌŁĖ껜³éČ”2ČĖ£¬ĒóĖł³éČ”µÄ2ČĖĄ“×ŌĶ¬Ņ»øö×éµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĖ«ĒśĻßC£ŗ ![]() ©
© ![]() =1£Øa£¾0£¬b£¾0£©Į½Ģõ½„½üĻßl1 £¬ l2ÓėÅ×ĪļĻßy2=©4xµÄ×¼Ļß1Ī§³ÉĒųÓņ¦ø£¬¶ŌÓŚĒųÓņ¦ø£Ø°üŗ¬±ß½ē£©£¬¶ŌÓŚĒųÓņ¦øÄŚČĪŅāŅ»µć£Øx£¬y£©£¬Čō
=1£Øa£¾0£¬b£¾0£©Į½Ģõ½„½üĻßl1 £¬ l2ÓėÅ×ĪļĻßy2=©4xµÄ×¼Ļß1Ī§³ÉĒųÓņ¦ø£¬¶ŌÓŚĒųÓņ¦ø£Ø°üŗ¬±ß½ē£©£¬¶ŌÓŚĒųÓņ¦øÄŚČĪŅāŅ»µć£Øx£¬y£©£¬Čō ![]() µÄ×ī“óÖµŠ”ÓŚ0£¬ŌņĖ«ĒśĻßCµÄĄėŠÄĀŹeµÄȔֵ·¶Ī§ĪŖ £®
µÄ×ī“óÖµŠ”ÓŚ0£¬ŌņĖ«ĒśĻßCµÄĄėŠÄĀŹeµÄȔֵ·¶Ī§ĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶÖŌ²![]() µÄĄėŠÄĀŹŹĒ
µÄĄėŠÄĀŹŹĒ![]() £¬¹żµć
£¬¹żµć![]() µÄ¶ÆÖ±Ļß
µÄ¶ÆÖ±Ļß![]() ÓėĶÖŌ²Ļą½»ÓŚ
ÓėĶÖŌ²Ļą½»ÓŚ![]() Į½µć£¬µ±Ö±Ļß
Į½µć£¬µ±Ö±Ļß![]() Óė
Óė![]() ÖįĘ½ŠŠŹ±£¬Ö±Ļß
ÖįĘ½ŠŠŹ±£¬Ö±Ļß![]() ±»ĶÖŌ²
±»ĶÖŌ²![]() ½ŲµĆµÄĻ߶Ī³¤ĪŖ
½ŲµĆµÄĻ߶Ī³¤ĪŖ![]() .
.
£Ø¢ń£©ĒóĶÖŌ²![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø¢ņ£©ŌŚ![]() ÖįÉĻŹĒ·ń“ęŌŚŅģÓŚµć
ÖįÉĻŹĒ·ń“ęŌŚŅģÓŚµć![]() µÄ¶Øµć
µÄ¶Øµć![]() £¬Ź¹µĆÖ±Ļß
£¬Ź¹µĆÖ±Ļß![]() ±ä»ÆŹ±£¬×ÜÓŠ
±ä»ÆŹ±£¬×ÜÓŠ![]() £æČō“ęŌŚ£¬Ēó³öµć
£æČō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčŗÆŹżf£Øx£©=|x+1|+|x©3|
£Ø1£©ĒóŗÆŹżf£Øx£©µÄ×īŠ”Öµ£»
£Ø2£©Čō{x|f£Øx£©”Üt2©3t}”É{x|©2”Üx”Ü0}”Ł£®Ē󏵏żtµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com