
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的单调增区间;
的单调增区间;
(2)令![]() .
.
①当![]() 时,若函数
时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
②当![]() 时,若
时,若![]() 的解集为
的解集为![]() ,且
,且![]() 中有且仅有一个整数,求实数b的取值范围.
中有且仅有一个整数,求实数b的取值范围.
【答案】(1)单调增区间是![]() 和
和![]() ; (2)①
; (2)①![]()
![]() .
.
【解析】
(1)先求导数,再解不等式得结果,(2)①根据题意得极值点函数值为零,解方程即得结果,②研究函数![]() 先分析
先分析![]() 中有解的必要条件,即最小值小于零,再结合图象确定有且仅有一个整数的条件,即得结果.
中有解的必要条件,即最小值小于零,再结合图象确定有且仅有一个整数的条件,即得结果.
(1)当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() 的单调增区间是
的单调增区间是![]() 和
和![]() .
.
(2)因为![]() .
.
①![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
因为函数![]() 有两个不同的零点,所以
有两个不同的零点,所以![]() 或
或![]() .
.
当![]() 时,得
时,得![]() ,不合题意,舍去;
,不合题意,舍去;
当![]() 时,代入得
时,代入得![]() ,
,
即![]() ,所以
,所以![]() .
.
②当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
所以在![]() 上,
上,![]() ,不合题意;
,不合题意;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
所以![]() ,
,
要使![]() 有解,首先要满足
有解,首先要满足![]() ,解得
,解得![]() . ①
. ①
又因为![]() ,
,![]() ,
,
要使![]() 的解集
的解集![]() 中只有一个整数,则
中只有一个整数,则![]()
即![]() 解得
解得![]() . ②
. ②
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递增;当
递增;当![]() 时,
时,![]() ,
,![]() 递减.
递减.
所以![]() ,所以
,所以![]() ,
,
所以由①和②得,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列命题中的说法正确的是( )
A. 若向量![]() ,则存在唯一的实数
,则存在唯一的实数![]() 使得
使得![]() ;
;
B. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
D. 命题“在![]() 中,
中,![]() 是
是![]() 的充要条件”的逆否命题为真命题.
的充要条件”的逆否命题为真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地村庄P与村庄O的距离为![]() 千米,从村庄O出发有两条道路
千米,从村庄O出发有两条道路![]() ,经测量,
,经测量,![]() 的夹角为
的夹角为![]() ,OP与
,OP与![]() 的夹角
的夹角![]() 满足
满足![]() (其中
(其中![]() ),现要经过P修一条直路分别与道路
),现要经过P修一条直路分别与道路![]() 交汇于
交汇于![]() 两点,并在
两点,并在![]() 处设立公共设施.
处设立公共设施.
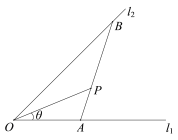
(1)已知修建道路![]() 的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点
的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点![]() 之间的距离;
之间的距离;
(2)考虑环境因素,需要对![]() 段道路进行翻修,
段道路进行翻修,![]() 段的翻修单价分别为n元/千米和
段的翻修单价分别为n元/千米和![]() 元/千米,要使两段道路的翻修总价最少,试确定
元/千米,要使两段道路的翻修总价最少,试确定![]() 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有3个白球,4个黑球,从中任取3个球,则
①恰有1个白球和全是白球;
②至少有1个白球和全是黑球;
③至少有1个白球和至少有2个白球;
④至少有1个白球和至少有1个黑球.
在上述事件中,是互斥事件但不是对立事件的为( )
A.②B.①C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.
的中点.
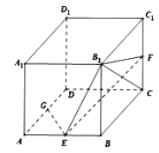
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣b)2=1(a>0)关于直线3x﹣2y=0对称,且与直线3x﹣4y+1=0相切.
(1)求圆C的方程;
(2)若直线l:y=kx+2与圆C交于M,N两点,是否存在直线l,使得![]() (O为坐标原点)若存在,求出k的值;若不存在,请说明理由.
(O为坐标原点)若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
| 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 5 | 4 | 2 |
已知![]() 和
和![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若每吨该农产品的成本为2.2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润![]() 取到最大值?
取到最大值?
参考公式:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com