【题目】对于给定的正整数
，如果各项均为正数的数列
满足：对任意正整数
，
总成立，那么称
是“
数列”．
（1）若
是各项均为正数的等比数列，判断
是否为“
数列”，并说明理由；
（2）若
既是“
数列”，又是“
数列”，求证： 
是等比数列．
【答案】（1）见解析；（2）见解析。
【解析】试题分析：（1）假设{an}是各项均为正数的等比数列，由等比数列的性质可得： 
即可证明．
（2）
既是“
数列”，又是“
数列”，可得
．可得
对于任意n∈N*（n≥4）都成立．即可证明．
试题解析：（1）
是“
数列”，理由如下：
因为
是各项均为正数的等比数列，不妨设公比为
．
当
时，有
所以
是“
数列”．
（2）因为
既是“
数列”，又是“
数列”，
所以
， 
， ①
， 
． ②
由①得， 
， 
， ③
， 
． ④
③
④
②得， 
， 
．
因为数列
各项均为正数，所以
， 
．
所以数列
从第3项起成等比数列，不妨设公比为
．
①中，令
得， 
，所以
．
①中，令
得， 
，所以
．
所以数列
是公比为
的等比数列．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】一个几何体的三视图如图所示，其中正视图与侧视图是腰长为6的等腰直角三角形，俯视图是正方形．
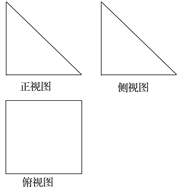
(1)请画出该几何体的直观图，并求出它的体积；
(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1?如何组拼？试证明你的结论；
(3)在(2)的情形下，设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.
表1：甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1：乙套设备的样本的频率分布直方图
（1）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ，求 |
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
为圆
的圆心， 
是圆上的动点，点
在圆的半径
上，且有点
和
上的点
，满足
， 
.
（1）当点
在圆上运动时，求点
的轨迹方程；
（2）若斜率为
的直线
与圆
相切，直线
与（1）中所求点
的轨迹交于不同的两点
， 
， 
是坐标原点，且
时，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x(1－
)是R上的偶函数．
(1)对任意的x∈[1,2]，不等式m·
≥2x＋1恒成立，求实数m的取值范围．
(2)令g(x)＝1－
，设函数F(x)＝g(4x－n)－g(2x＋1－3)有零点，求实数n的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直角三角形
中，
是
的中点，
是线段
上一个动点，且
，如图所示，沿
将
翻折至
，使得平面
平面
．
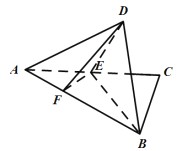
（1）当
时，证明：
平面
；
（2）是否存在
，使得
与平面
所成的角的正弦值是
？若存在，求出的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
