
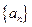 满足,
满足,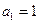 ,
,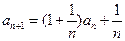 (n∈N*)。
(n∈N*)。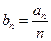 ,求数列
,求数列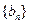 的通项公式;
的通项公式; 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
 时,求Sn.
时,求Sn.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
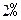 并按复利计算,问每年应该存入多少钱?
并按复利计算,问每年应该存入多少钱?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
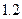 元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?
元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
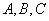 的机动车辆数如图所示(20,30;35,30;55,50),图中
的机动车辆数如图所示(20,30;35,30;55,50),图中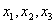 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段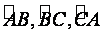 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )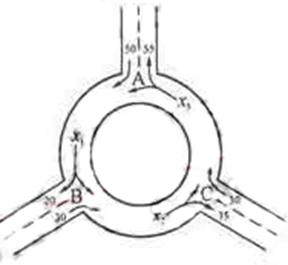
A.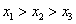 | B.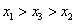 |
C.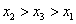 | D.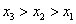 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com