
【题目】下列说法中正确的个数是( )
(1)已知沙坪坝明天刮风的概率P(A)=0.5,下雨的概率![]() =0.3,则沙坪坝明天又刮风又下雨的概率
=0.3,则沙坪坝明天又刮风又下雨的概率 ![]() .
.
(2)命题 p :直线ax y 1 0 和3x (a 2) y 3 0 平行; 命题 q : a 3 .则 q 是 p 的必要条件.
(3)![]() 被7 除后所得的余数为5.
被7 除后所得的余数为5.
(4) 已知i 是虚数单位,![]() 复数
复数![]() ,则
,则![]() 最小值是2.
最小值是2.
A.1B.2C.3D.4
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为
的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县应国家号召,积极开展了建设新农村活动,实行以奖代补,并组织有关部门围绕新农村建设中的三个方面(新设施,新环境,新风尚)对各个村进行综合评分,高分(大于88分)的村先给予5万元的基础奖励,然后比88分每高一分,奖励增加5千元,低分(小于等于75分)的村给予通报,取消5万元的基础奖励,且比75分每低1分,还要扣款1万元,并要求重新整改建设,分数在![]() 之间的只享受5万元的基础奖励,下面是甲、乙两个乡镇各10个村的得分数据(单位:分):
之间的只享受5万元的基础奖励,下面是甲、乙两个乡镇各10个村的得分数据(单位:分):
甲:62,74,86,68,97,75,88,98,76,99;
乙:71,81,72,86,91,77,85,78,83,84.
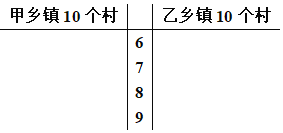
(1)根据上述数据完成如图的茎叶图,并通过茎叶图比较两个乡镇各10个村的得分的平均值及分散程度;(不要求计算具体的数值,只给出结论即可)
(2)为继续做好新农村的建设工作,某部门决定在这两个乡镇中任选两个低分村进行帮扶重建,求抽取的两个村中,两个乡镇中各有一个村的概率;
(3)从获取奖励的角度看,甲、乙两个乡镇哪个获取的奖励多?(需写出计算过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 〔
〔![]() >b>0〕与抛物线
>b>0〕与抛物线![]() 有共同的焦点F,且两曲线在第一象限的交点为M,满足
有共同的焦点F,且两曲线在第一象限的交点为M,满足![]() .
.
(1)求椭圆的方程;
(2)过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,设
两点,设![]() ,假设
,假设![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,昆明加大了特色农业建设,其中花卉产业是重要组成部分.昆明斗南毗邻滇池东岸,是著名的花都,有“全国10支鲜花7支产自斗南”之说,享有“金斗南”的美誉.为进一步了解鲜花品种的销售情况,现随机抽取甲、乙两户斗南花农,对其连续5日的玫瑰花日销售情况进行跟踪调查,将日销售量作为样本绘制成茎叶图如下,单位:扎(20支/扎).
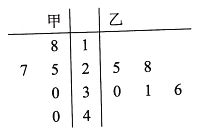
(1)求甲、乙两户花农连续5日的日均销售量,并比较两户花农连续5日销售量的稳定性;
(2)从两户花农连续5日的销售量中各随机抽取一个,求甲的销售量比乙的销售量高的概率·
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com