
【题目】已知直线y=k(x+3)(k>0)与抛物线C:y2=12x相交于A,B两点,F为C的焦点,若|FA|=3|FB|,则k的值等于_____.
【答案】![]()
【解析】
设A(x1,y1),B(x2,y2).联立方程化为k2x2+(6k2-12)x+9k2=0,(k>0).根据根与系数的关系,利用抛物线的定义可得:|FA|=x1+3,|FB|=x2+3,利用|FA|=3|FB|,联立解出即可
设A(x1,y1),B(x2,y2).易知F(3,0)

联立直线y=k(x+3)(k>0)与抛物线C:y2=12x,
化为k2x2+(6k2-12)x+9k2=0,(k>0).
∴x1+x2=![]() -6 ①,x1x2=9 ②.
-6 ①,x1x2=9 ②.
∵|FA|=3|FB|,根据抛物线的定义,可得 |FA|=x1+3,|FB|=x2+3,
∴x1+3=3(x2+3)③,化为x1=3x2+6.
联立①②③,解得k=![]()


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】某学生社团对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排进行分层抽样,并完成一项试验,试验方法是:使两组学生记忆40个无意义音节(如xiq,geh),均要求刚能全部记清就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点不含右端点)。
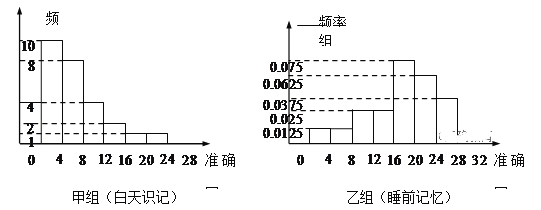
(1)估计1000名被调查的学生中识记停止8小时后40个音节的保持率大于或等于60%的人数;
(2)从乙组准确回忆个数在![]() 范围内的学生中随机选3人,记:能准确回忆20个以上(含20)的人数为随机变量X,求X的分布列及数学期望;
范围内的学生中随机选3人,记:能准确回忆20个以上(含20)的人数为随机变量X,求X的分布列及数学期望;
(3)从本次试验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好?计算并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E是棱DD1的中点.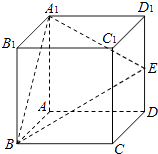
(1)求直线BE与平面ABB1A1所成的角的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M的对称轴为坐标轴,离心率为![]() ,且一个焦点坐标为(
,且一个焦点坐标为(![]() ,0).
,0).
(1)求椭圆M的方程;
(2)设直线l与椭圆M相交于A,B两点,以线段OA,OB为邻边作平行四边形OAPB,其中点P在椭圆M上,O为坐标原点,求点O到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex[ ![]() x3﹣2x2+(a+4)x﹣2a﹣4],其中a∈R,e为自然对数的底数.
x3﹣2x2+(a+4)x﹣2a﹣4],其中a∈R,e为自然对数的底数.
(1)若函数f(x)的图象在x=0处的切线与直线x+y=0垂直,求a的值;
(2)关于x的不等式f(x)<﹣ ![]() ex在(﹣∞,2)上恒成立,求a的取值范围;
ex在(﹣∞,2)上恒成立,求a的取值范围;
(3)讨论函数f(x)极值点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆C的圆心C( ![]() ,
, ![]() ),半径r=
),半径r= ![]() .
.
(1)求圆C的极坐标方程;
(2)若α∈[0, ![]() ),直线l的参数方程为
),直线l的参数方程为 ![]() (t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
(t为参数),直线l交圆C于A、B两点,求弦长|AB|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com