
设命题甲:关于 的不等式
的不等式 对一切
对一切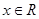 恒成立,命题乙:对数函数
恒成立,命题乙:对数函数 在
在 上递减,那么甲是乙的(
)
上递减,那么甲是乙的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:2013届福建省高二下学期第一次阶段考数学理科试卷 题型:解答题
已知命题p:关于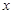 的不等式
的不等式 对一切
对一切 恒成立,命题q:函数
恒成立,命题q:函数 是增函数,若p或q为真,p且q为假,求实数
是增函数,若p或q为真,p且q为假,求实数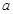 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出两个命题:
命题甲:关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ;
;
命题乙:函数![]() 为增函数。
为增函数。
分别求出符合下列条件的实数a的取值范围:
(1)甲,乙至少有一个是真命题;
(2)甲,乙中有且只有一个是真命题。
查看答案和解析>>
科目:高中数学 来源:广东深圳高级中学09-10学年度高二第二学期期末考试理 题型:填空题
设命题P:关于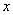 的不等式
的不等式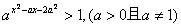 的解集为
的解集为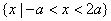 ;命题Q:
;命题Q: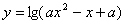 的定义域为R,如果P、Q有且仅有一个正确,则
的定义域为R,如果P、Q有且仅有一个正确,则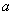 的取值范围是 。
的取值范围是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com