
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
【答案】(1)分布列见解析;(2)![]() ,462次;
,462次;![]() ,404次;
,404次;![]() ,397次;272次
,397次;272次
【解析】
(1)由题得![]() ,
,![]() ,分别求出对应的概率即得
,分别求出对应的概率即得![]() 的分布列;
的分布列;
(2)先求出![]() ,再分别求出
,再分别求出![]() 分别取2,3,4时,各需化验的平均总次数,即得相比方案一,化验次数最多可以平均减少的次数.
分别取2,3,4时,各需化验的平均总次数,即得相比方案一,化验次数最多可以平均减少的次数.
(1)设每个人的血呈阴性反应的概率为![]() ,则
,则![]() .
.
所以![]() 个人的血混合后呈阴性反应的概率为
个人的血混合后呈阴性反应的概率为![]() ,呈阳性反应的概率为
,呈阳性反应的概率为![]() .
.
依题意可知![]() ,
,![]() ,
,
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
(2)方案二中,结合(1)知每个人的平均化验次数为
![]() ,
,
所以当![]() 时,
时,![]() ,
,
此时669人需要化验的总次数为462次;
当![]() 时,
时,![]() ,
,
此时669人需要化验的总次数为404次;
当![]() 时,
时,![]() ,
,
此时669人需要化验的总次数为397次.
即![]() 时化验次数最多,
时化验次数最多,![]() 时次数居中,
时次数居中,![]() 时化验次数最少,
时化验次数最少,
而采用方案一则需化验669次.
故在这三种分组情况下,
相比方案一,当![]() 时化验次数最多可以平均减少
时化验次数最多可以平均减少![]() (次)
(次)


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
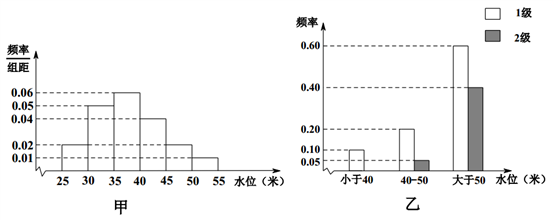
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京地铁八通线西起四惠站,东至土桥站,全长18.964km,共设13座车站.目前八通线执行2014年12月28日制订的计价标准,各站间计程票价(单位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | /p> | 3 | 3 | ||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
(Ⅰ)在13座车站中任选两个不同的车站,求两站间票价不足5元的概率;
(Ⅱ)甲乙二人从四惠站上车乘坐八通线,各自任选另一站下车(二人可同站下车),记甲乙二人乘车购票花费之和为X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通线,甲从四惠站上车,任选另一站下车,记票价为![]() 元;乙从土桥站上车,任选另一站下车,记票价为
元;乙从土桥站上车,任选另一站下车,记票价为![]() 元.试比较
元.试比较![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(结论不需要证明)
大小.(结论不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,
,![]() ,在平行四边形
,在平行四边形![]() 中,
中,![]() ,Q为
,Q为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点E、F,且
于点E、F,且![]() 平面
平面![]() .
.
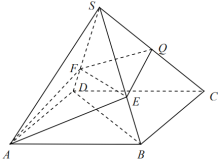
(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,Q为
,Q为![]() 的中点,
的中点,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为直角坐标原点,以极轴为
为直角坐标原点,以极轴为![]() 轴的正半轴建立平面直角坐标系
轴的正半轴建立平面直角坐标系![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的
个单位长度,再将得到的曲线上的每一个点的横坐标缩短为原来的![]() ,纵坐标保持不变,得到曲线
,纵坐标保持不变,得到曲线![]()
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是空间两条不同的直线,
是空间两条不同的直线,![]() 、
、![]() 是空间两个不同的平面.给出下列四个命题:
是空间两个不同的平面.给出下列四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某学校组织教师进行“学习强国”知识竞赛,规则为:每位参赛教师都要回答3个问题,且对这三个问题回答正确与否相互之间互不影响,若每答对1个问题,得1分;答错,得0分,最后按照得分多少排出名次,并分一、二、三等奖分别给予奖励.已知对给出的3个问题,教师甲答对的概率分别为![]() ,
,![]() ,p.若教师甲恰好答对3个问题的概率是
,p.若教师甲恰好答对3个问题的概率是![]() ,则
,则![]() ________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com