
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)是否存在![]() ,使得
,使得![]() 在区间
在区间![]() 的最小值为
的最小值为![]() 且最大值为1?若存在,求出
且最大值为1?若存在,求出![]() 的所有值;若不存在,说明理由.
的所有值;若不存在,说明理由.
【答案】(1)见详解;(2) ![]() 或
或![]() .
.
【解析】
(1)先求![]() 的导数,再根据
的导数,再根据![]() 的范围分情况讨论函数单调性;(2) 根据
的范围分情况讨论函数单调性;(2) 根据![]() 的各种范围,利用函数单调性进行最大值和最小值的判断,最终得出
的各种范围,利用函数单调性进行最大值和最小值的判断,最终得出![]() ,
,![]() 的值.
的值.
(1)对![]() 求导得
求导得![]() .所以有
.所以有
当![]() 时,
时,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增;
区间上单调递增;
当![]() 时,
时,![]() 区间上单调递增;
区间上单调递增;
当![]() 时,
时,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增.
区间上单调递增.
(2)若![]() 在区间
在区间![]() 有最大值1和最小值-1,所以
有最大值1和最小值-1,所以
若![]() ,
,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增;
区间上单调递增;
此时在区间![]() 上单调递增,所以
上单调递增,所以![]() ,
,![]() 代入解得
代入解得![]() ,
,![]() ,与
,与![]() 矛盾,所以
矛盾,所以![]() 不成立.
不成立.
若![]() ,
,![]() 区间上单调递增;在区间
区间上单调递增;在区间![]() .所以
.所以![]() ,
,![]() 代入解得
代入解得 ![]() .
.
若![]() ,
,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增.
区间上单调递增.
即![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,所以区间
单调递增,所以区间![]() 上最小值为
上最小值为![]()
而![]() ,故所以区间
,故所以区间![]() 上最大值为
上最大值为![]() .
.
即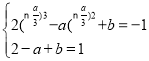 相减得
相减得![]() ,即
,即![]() ,又因为
,又因为![]() ,所以无解.
,所以无解.
若![]() ,
,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增.
区间上单调递增.
即![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增,所以区间
单调递增,所以区间![]() 上最小值为
上最小值为![]()
而![]() ,故所以区间
,故所以区间![]() 上最大值为
上最大值为![]() .
.
即 相减得
相减得![]() ,解得
,解得![]() ,又因为
,又因为![]() ,所以无解.
,所以无解.
若![]() ,
,![]() 区间上单调递增,
区间上单调递增,![]() 区间上单调递减,
区间上单调递减,![]() 区间上单调递增.
区间上单调递增.
所以有![]() 区间
区间![]() 上单调递减,所以区间
上单调递减,所以区间![]() 上最大值为
上最大值为![]() ,最小值为
,最小值为![]()
即![]() 解得
解得![]() .
.
综上得![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分![]() 分),现有甲、乙两班本次考试数学分数如下列茎叶图所示:
分),现有甲、乙两班本次考试数学分数如下列茎叶图所示:

(1)根据茎叶图求甲、乙两班同学成绩的中位数,并将以班同学的成绩的频率分布直方图填充完整;

(2)根据茎叶图比较在一模考试中,甲、乙两班同学数学成绩的平均水平和分数的分散程度(不要求计算出具体值,给出结论即可);
(3)若规定分数在![]() 的成绩为良好,分数在
的成绩为良好,分数在![]() 的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出
的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出![]() 位同学参加数学提优培训,求这
位同学参加数学提优培训,求这![]() 位同学中恰含甲、乙两班所有
位同学中恰含甲、乙两班所有![]() 分以上的同学的概率.
分以上的同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,![]() )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时, f(x)=-x+1
(1)求f(0),f(2);
(2)求函数f(x)的解析式;
(3)若f(a-1)<3,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com