练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学校有教职员工150人，其中高级职称15人，中级职称45人，一般职员90人，现在用分层抽样抽取30人，则样本中各职称人数分别为（ ）
    A.5，10，15
    B.3，9，18
    C.3，10，17
    D.5，9，16

    【答案】B
    【解析】解：由 = ，

    所以，高级职称人数为15× =3（人）；

    中级职称人数为45× =9（人）；

    一般职员人数为90× =18（人）．

    所以高级职称人数、中级职称人数及一般职员人数依次为3，9，18．

    故选B．

    【考点精析】本题主要考查了分层抽样的相关知识点，需要掌握先将总体中的所有单位按照某种特征或标志（性别、年龄等）划分成若干类型或层次，然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本，最后，将这些子样本合起来构成总体的样本才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直棱柱ABC﹣A1B1C1中，AC=BC=CC1= AB，E是线段CC1的中点，连接AE，B1E，AB1 ， B1C，BC1 ， 得到的图形如图所示． （Ⅰ）证明BC1⊥平面AB1C；
    （Ⅱ）求二面角E﹣AB1﹣C的大小．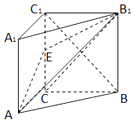

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某港口的水深y（米）是时间t（0≤t≤24，单位：小时）的函数，下面是每天时间与水深的关系表：

    t

    0

    3

    6

    9

    12

    15

    18

    21

    24

    y

    10

    13

    9.9

    7

    10

    13

    10.1

    7

    10

    经过长期观测，y=f（t）可近似的看成是函数y=Asinωt+b
    （1）根据以上数据，求出y=f（t）的解析式；
    （2）若船舶航行时，水深至少要11.5米才是安全的，那么船舶在一天中的哪几段时间可以安全的进出该港？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知首项都是1的两个数列{an}，{bn} 满足anbn+1﹣an+1bn﹣2an+1an=0．
    （1）令 ，求证数列{cn}为等差数列；
    （2）若 ，求数列{bn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，﹣＜φ＜ ， x∈R）的部分图象如图所示．
    （1）求函数y=f（x）的解析式；
    （2）当x∈[﹣ ， ]时，求f（x）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某人射击一次命中7～10环的概率如下表

    命中环数

    7

    8

    9

    10

    命中概率

    0.16

    0.19

    0.28

    0.24

    计算这名射手在一次射击中：
    （1）射中10环或9环的概率；
    （2）至少射中7环的概率；
    （3）射中环数不足8环的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长都相等的四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是 ( )
    A.BC∥平面PDF
    B.DF⊥平面PAE
    C.平面PDF⊥平面ABC
    D.平面PAE⊥平面ABC

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝(m2－m－1)x－5m－3 ， m为何值时，f(x)：
    （1）是幂函数；
    （2）是正比例函数；
    （3）是反比例函数；
    （4）是二次函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解关于x的不等式：（x﹣1）（x+a）＞0．

    查看答案和解析>>

    同步练习册答案