
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点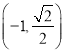 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为![]() ,定点
,定点![]() ,过点
,过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 的另一个交点为
的另一个交点为![]() ,试探究在
,试探究在![]() 轴上是否存在一定点
轴上是否存在一定点![]() ,使直线
,使直线![]() 恒过该定点,若存在,求出该定点的坐标;若不存在,请说明理由.
恒过该定点,若存在,求出该定点的坐标;若不存在,请说明理由.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
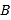
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某有机水果种植基地试验种植的某水果在售卖前要成箱包装,每箱80个,每一箱水果在交付顾客之前要按约定标准对水果作检测,如检测出不合格品,则更换为合格品.检测时,先从这一箱水果中任取10个作检测,再根据检测结果决定是否对余下的所有水果作检测.设每个水果为不合格品的概率都为![]() ,且各个水果是否为不合格品相互独立.
,且各个水果是否为不合格品相互独立.
(Ⅰ)记10个水果中恰有2个不合格品的概率为![]() ,求
,求![]() 取最大值时p的值
取最大值时p的值![]() ;
;
(Ⅱ)现对一箱水果检验了10个,结果恰有2个不合格,以(Ⅰ)中确定的![]() 作为p的值.已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a元的赔偿费用
作为p的值.已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a元的赔偿费用![]() .
.
(ⅰ)若不对该箱余下的水果作检验,这一箱水果的检验费用与赔偿费用的和记为X,求EX;
(ⅱ)以检验费用与赔偿费用和的期望值为决策依据,当种植基地要对每个不合格水果支付的赔偿费用至少为多少元时,将促使种植基地对这箱余下的所有水果作检验?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知斜率存在且不为0的直线![]() 过点
过点![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,椭圆
两点,椭圆![]() 的左顶点为
的左顶点为![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,且
,且![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .探究:
.探究:![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com