
分析 由题意分直线l的斜率存在和不存在分析,当直线l的斜率不存在时,求出M,N的坐标,由向量数量积为0可得∠MON=$\frac{π}{2}$;当直线的斜率不存在时,设出直线l的方程,和椭圆方程联立,化为关于x的一元二次方程,借助于根与系数的关系及平面向量数量积的运算求得$∠MON=\frac{π}{2}$.
解答 解:当直线l与与圆O相切时,且斜率不存在时,直线方程为x=$±\frac{1}{5}$,
当直线方程为x=$\frac{1}{5}$时,可得两点坐标为($\frac{1}{5},\frac{1}{5}$),($\frac{1}{5},-\frac{1}{5}$),
∵$\overrightarrow{OM}•\overrightarrow{ON}=0$,∴∠MON=$\frac{π}{2}$;同理当x=-$\frac{1}{5}$时,∠MON=$\frac{π}{2}$;
当直线l与x轴不垂直时,设直线方程为y=kx+b,
由直线与圆相切,可得d=$\frac{|b|}{\sqrt{{k}^{2}+1}}$=$\frac{1}{5}$,即25b2=k2+1 ①,
联立$\left\{\begin{array}{l}{y=kx+b}\\{9{x}^{2}+16{y}^{2}=1}\end{array}\right.$,得(9+16k2)x2+32kbx+16b2-1=0.
△>0,${x}_{1}+{x}_{2}=-\frac{32kb}{9+16{k}^{2}},{x}_{1}{x}_{2}=\frac{16{b}^{2}-1}{9+16{k}^{2}}$,
由$\overrightarrow{OM}•\overrightarrow{ON}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}$=x1x2+(kx1+b)(kx2+b)
=$(1+{k}^{2}){x}_{1}{x}_{2}+kb({x}_{1}+{x}_{2})+{b}^{2}=\frac{25{b}^{2}-{k}^{2}-1}{9+16{k}^{2}}$ ②,
由①②得$\overrightarrow{OM}•\overrightarrow{ON}=0$,即$∠MON=\frac{π}{2}$.
综上,∠MON=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查椭圆的简单性质,考查了平面向量在解题中的应用,是中档题.


科目:高中数学 来源: 题型:解答题
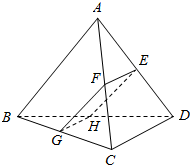 如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.
如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com