
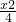 +
+ =1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程.
=1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程. ,0),l:x=-2
,0),l:x=-2 ,离心率e=
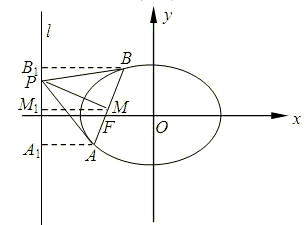
,离心率e= .设过点F的弦AB的中点为M,分别过A,B,M向准线l作垂线,垂足分别为A1,B1,M1,则|MM1|=
.设过点F的弦AB的中点为M,分别过A,B,M向准线l作垂线,垂足分别为A1,B1,M1,则|MM1|= (|AA1|+|BB1|)=
(|AA1|+|BB1|)= (
(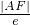 +
+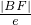 )=
)= |AB|,又因为△PAB为等边三角形?|PM|=
|AB|,又因为△PAB为等边三角形?|PM|= |AB|,所以
|AB|,所以 =
= ,
,
 ,
, ,tam∠PMM1=
,tam∠PMM1= ,
,
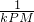 =±
=± ,
, ,0),所以AB的方程为y=±
,0),所以AB的方程为y=± (x+
(x+ ).
). ,或
,或 .
. (|AA1|+|BB1|)=
(|AA1|+|BB1|)= (
(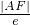 +
+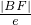 )=
)= |AB|,又因为△PAB为等边三角形?|PM|=
|AB|,又因为△PAB为等边三角形?|PM|= |AB|,所以
|AB|,所以 =
= ,cos∠PMM1=
,cos∠PMM1= ,由此能求出AB的方程.
,由此能求出AB的方程.

科目:高中数学 来源: 题型:
| y2 |
| 4 |
| 5 |
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| F1P |
| F1Q |
查看答案和解析>>
科目:高中数学 来源:2006-2007学年江苏省南京市金陵中学高三数学综合试卷(解析版) 题型:解答题
 +
+ =1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程.
=1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程.查看答案和解析>>
科目:高中数学 来源:2007年江苏省南京市高考数学模拟试卷(解析版) 题型:解答题
 +
+ =1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程.
=1的左焦点为F,左准线为l,一条直线过点F与椭圆C交于A,B两点,若直线l上存在点P,使△ABP为等边三角形,求直线AB的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com