
【题目】已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为 ![]()

(1)求椭圆的方程;
(2)若A(0,1),设M,N是椭圆上异于点A的任意两点,且AM⊥AN,线段MN的中垂线l与x轴的交点为(m,0),求m的取值范围.
【答案】
(1)解:设椭圆的方程为 ![]() +
+ ![]() =1(a>b>0),
=1(a>b>0),
可得a=2,e= ![]() =
= ![]() ,解得c=
,解得c= ![]() ,
,
b= ![]() =1,
=1,
即有椭圆的方程为 ![]() +y2=1;
+y2=1;
(2)解:设M(x1,y1),N(x2,y2),MN的中点的横坐标为 ![]() ,
,
由直线y=kx+t代入椭圆方程x2+4y2=4,可得
(1+4k2)x2+8ktx+4t2﹣4=0,
△=64k2t2﹣16(1+4k2)(4t2﹣4)>0,即1+4k2>t2,
x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
可得MN的中点坐标为(﹣ ![]() ,
, ![]() ),
),
中垂线方程为y﹣ ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() ),
),
令y=0,可得x=m=﹣ ![]() ,
,
由AM⊥AN,可得 ![]()
![]() =﹣1,
=﹣1,
即为(1+k2)x1x2+(t﹣1)2+k(t﹣1)(x1+x2)=0,
化为(1+k2)(4t2﹣4)+(t﹣1)2(1+4k2)+4(t﹣1)(﹣8kt)=0,
解得t=1或﹣ ![]() ,显然满足判别式大于0.
,显然满足判别式大于0.
即有m=﹣ ![]() 或
或 ![]() ,
,
当k=0时,m=0;
当k>0时,m= ![]() ≥﹣
≥﹣ ![]() =﹣
=﹣ ![]() ,即为﹣
,即为﹣ ![]() ≤m<0;
≤m<0;
或m= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() ,即为0<m≤
,即为0<m≤ ![]() ;
;
同样当k<0时,可得0<m≤ ![]() 或﹣
或﹣ ![]() ≤m<0.
≤m<0.
综上可得m的范围是[﹣ ![]() ,
, ![]() ]∪[﹣
]∪[﹣ ![]() ,
, ![]() ]
]
【解析】(1)设椭圆的方程为 ![]() +
+ ![]() =1(a>b>0),运用离心率公式,以及a,b,c的关系,可得b,进而得到椭圆方程;(2)设M(x1 , y1),N(x2 , y2),MN的中点的横坐标为
=1(a>b>0),运用离心率公式,以及a,b,c的关系,可得b,进而得到椭圆方程;(2)设M(x1 , y1),N(x2 , y2),MN的中点的横坐标为 ![]() ,由直线y=kx+t代入椭圆方程x2+4y2=4,可得(1+4k2)x2+8ktx+4t2﹣4=0,运用判别式大于0和韦达定理,结合两直线垂直的条件:斜率之积为﹣1,由基本不等式可得最值,进而得到所求范围.
,由直线y=kx+t代入椭圆方程x2+4y2=4,可得(1+4k2)x2+8ktx+4t2﹣4=0,运用判别式大于0和韦达定理,结合两直线垂直的条件:斜率之积为﹣1,由基本不等式可得最值,进而得到所求范围.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点.
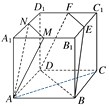
(1)求MN与AC所成角,并说明理由.
(2)求证:平面AMN∥平面EFDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=8x的焦点为F,过点F作直线l与抛物线分别交于A,B两点,若点M满足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),过M作y轴的垂线与抛物线交于点P,若|PF|=4,则M点的横坐标为 .
),过M作y轴的垂线与抛物线交于点P,若|PF|=4,则M点的横坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年中华人民共和国环境保护部批准《环境空气质量标准》为国家环境质量标准,该标准增设和调整了颗粒物、二氧化氮、铅、笨等的浓度限值,并从2016年1月1日起在全国实施.空气质量的好坏由空气质量指数确定,空气质量指数越高,代表空气污染越严重,某市对市辖的某两个区加大了对空气质量的治理力度,从2015年11月1日起监测了100天的空气质量指数,并按照空气质量指数划分为:指标小于或等于115为通过,并引进项目投资.大于115为未通过,并进行治理.现统计如下.
空气质量指数 | (0,35] | [35,75] | (75,115] | (115,150] | (150,250] | >250 |
空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲区天数 | 13 | 20 | 42 | 20 | 3 | 2 |
乙区天数 | 8 | 32 | 40 | 16 | 2 | 2 |
(1)以频率值作为概率值,求甲区和乙区通过监测的概率;
(2)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元)..在(1)的前提下,记X为通过监测,引进项目增加的税收总额,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求证:AC是∠DAB的平分线;
(2)求证:OF∥AG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图. 
(1)估计在40名广场舞者中年龄分布在[40,70)的人数;
(2)求40名广场舞者年龄的中位数和平均数的估计值;
(3)若从年龄在[20,40)中的广场舞者中任取2名,求这两名广场舞者年龄在[30,40)中的人数X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com