
【题目】已知抛物线![]() 的焦点为F,且过点A (2,2),椭圆
的焦点为F,且过点A (2,2),椭圆![]() 的离心率为
的离心率为![]() ,点B为抛物线C与椭圆D的一个公共点,且
,点B为抛物线C与椭圆D的一个公共点,且![]() .
.
(Ⅰ)求椭圆D的方程;
(Ⅱ)过椭圆内一点P(0,t)的直线l的斜率为k,且与椭圆C交于M,N两点,设直线OM,ON(O为坐标原点)的斜率分别为k1,k2,若对任意k,存在实数λ,使得k1+ k2=λk,求实数λ的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(Ⅰ)由点A(2,2)在拋物线![]() 上,得
上,得![]() 所以抛物线C的方程为
所以抛物线C的方程为![]() ,其焦点F(0,
,其焦点F(0, ![]() ),设B(m,n),则由抛物线的定义可得|BF| =
),设B(m,n),则由抛物线的定义可得|BF| = ![]() ,解得
,解得![]() ,代入抛物线方程可得m=±
,代入抛物线方程可得m=±![]() ,所以B(±
,所以B(±![]() ,1),椭圆C的离心率
,1),椭圆C的离心率![]() ,所以
,所以![]() ,又点B(±
,又点B(±![]() ,1)在椭圆上,可得
,1)在椭圆上,可得![]() 的值即得椭圆D的方程;
的值即得椭圆D的方程;
(Ⅱ) 设直线l的方程为![]() . 由
. 由 ,消元可得
,消元可得![]() ,根据韦达定理得
,根据韦达定理得![]() ,因为此等式对任意的
,因为此等式对任意的![]() 都成立,所以
都成立,所以![]() ,即
,即![]() . 由题意得点P(0,t)在椭圆内,故0≤t2<2,即0≤
. 由题意得点P(0,t)在椭圆内,故0≤t2<2,即0≤![]() <2可解得实数λ的取值范围.
<2可解得实数λ的取值范围.
试题解析:
(Ⅰ)由点A(2,2)在拋物线![]() 上,得
上,得![]() ,解得
,解得![]()
所以抛物线C的方程为![]() ,其焦点F(0,
,其焦点F(0, ![]() ),
),
设B(m,n),则由抛物线的定义可得|BF| = ![]() ,解得
,解得![]() ,
,
代入抛物线方程可得m2=2n = 2,解得m=±![]() ,所以B(±
,所以B(±![]() ,1),
,1),
椭圆C的离心率![]() ,所以
,所以![]() ,
,
又点B(±![]() ,1)在椭圆上,所以
,1)在椭圆上,所以![]() ,解得
,解得![]() ,
,
所以椭圆D的方程为![]() .
.
(Ⅱ)设直线l的方程为![]() .
.
由 ,消元可得
,消元可得![]() ,
,
设M(x1 , y1 ) , N(x2,y2),则![]() ,
,
而![]() ,由
,由![]() ,得
,得![]() ,
,
因为此等式对任意的![]() 都成立,所以
都成立,所以![]() ,即
,即![]() .
.
由题意得点P(0,t)在椭圆内,故0≤t2<2,即0≤![]() <2,解得
<2,解得![]() .
.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ,顶点
,顶点![]() 在底面
在底面![]() 上的射影恰为点
上的射影恰为点![]() ,且
,且![]()
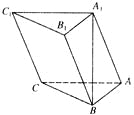
(1)证明:平面![]()
![]() 平面
平面![]() ;
;
(2)求棱![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(3)若点![]() 为
为![]() 的中点,并求出二面角
的中点,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() :
: ![]() 的焦点,点
的焦点,点![]() 是准线
是准线![]() 上的动点,直线
上的动点,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,若点
两点,若点![]() 的纵坐标为
的纵坐标为![]() ,点
,点![]() 为准线
为准线![]() 与
与![]() 轴的交点.
轴的交点.

(1)求直线![]() 的方程;
的方程;
(2)求![]() 的面积
的面积![]() 范围.
范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,记点P到点A(-1,1)的距离与点P到直线x= - 1的距离之和的最小值为M,若B(3,2),记|PB|+|PF|的最小值为N,则M+N= ______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90)内)分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90).得到频率分布直方图如图C34.
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组学生中用分层抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 关于坐标轴对称,以坐标原点
关于坐标轴对称,以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系, ![]() ,
, ![]() 为椭圆
为椭圆![]() 上两点.
上两点.
(1)求直线![]() 的直角坐标方程与椭圆
的直角坐标方程与椭圆![]() 的参数方程;
的参数方程;
(2)若点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 在第一象限内,求四边形
在第一象限内,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com