
| A. | |t1-t2| | B. | $\sqrt{{a^2}+{b^2}}|{{t_1}-{t_2}}|$ | C. | $\frac{{|{{t_1}-{t_2}}|}}{{\sqrt{{a^2}+{b^2}}}}$ | D. | $\frac{{|{{t_1}-{t_2}}|}}{{{a^2}+{b^2}}}$ |
分析 由|AB|2=[(x0+at1)-(x0+at2)]2[(y0+bt1)-(y0+bt2)]2,能求出|AB|的表达式.
解答 解:∵直线$\left\{\begin{array}{l}x={x_0}+at\\ y={y_0}+bt\end{array}\right.$(t为参数)上的两个点A,B对应参数分别为t1,t2,
∴|AB|2=[(x0+at1)-(x0+at2)]2+[(y0+bt1)-(y0+bt2)]2
=(at1-at2)2+(bt1-bt2)2
=(a2+b2)(t1-t2)2,
∴|AB|=$\sqrt{{a}^{2}+{b}^{2}}$|t1-t2|.
故选:B.
点评 本题考查两点间距离公式的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | N<P<M | B. | N<P≤M | C. | N<M<P | D. | N<M≤P |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
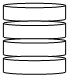 小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是$\frac{7}{8}$.
小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD内接于抛物线x2=y,点C(3,9),AC平行于x轴,BD平行于该抛物线在点C处的切线,∠BAD=90°.
如图,已知四边形ABCD内接于抛物线x2=y,点C(3,9),AC平行于x轴,BD平行于该抛物线在点C处的切线,∠BAD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com