
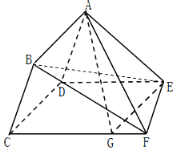
【题目】如图,在多面体ABCDEF中,四边形ABCD为平行四边形,平面ADE⊥平面CDEF,∠ADE=60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=4,点G是棱CF上的动点.
(Ⅰ)当CG=3时,求证EG∥平面ABF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值;
(Ⅲ)若二面角G﹣AE﹣D所成角的余弦值为![]() ,求线段CG的长.
,求线段CG的长.
【答案】(Ⅰ)证明见详解;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(1)通过证明直线AB∥EG,从而由线线平行推证线面平行;
(2)过A作DE垂线AO,以![]() 为坐标原点,建立空间直角坐标系,求出平面的法向量以及直线的方向向量,从而求解线面角的正弦值;
为坐标原点,建立空间直角坐标系,求出平面的法向量以及直线的方向向量,从而求解线面角的正弦值;
(3)由(2)中所建的直角坐标系,根据二面角G﹣AE﹣D所成角的余弦值,求得G点的坐标,即可求得CG的长度.
(Ⅰ)证明:由已知得CG∥DE且CG=DE,
故四边形CDEG为平行四边形,
∴CD∥EG,
∵四边形ABCD为平行四边形,
∴CD∥AB,∴AB∥EG,
又EG平面ABF,AB平面ABF,
∴EG∥平面ABF.
(Ⅱ)过点A作AO⊥DE交DE于点O,过点O作OK∥CD交CF于点K
由(1)知平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE,AO平面ADE,
∴AO⊥平面CDEF,∵CD⊥DE,∴OK⊥DE,以O为原点建立如图的空间直角坐标系,
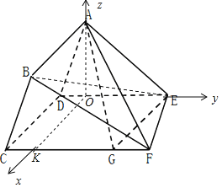
则D(0,﹣1,0),E(0,2,0),C(3,﹣1,0),
F(3,3,0),![]() ,D(0,﹣1,0),
,D(0,﹣1,0),
∴![]()
设平面ABCD的法向量为![]() ,
,
即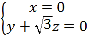 ,令z=﹣1,则
,令z=﹣1,则![]() ,
,
![]() ,
,
∴直线BE与平面ABCD所成角的正弦值为![]() ,
,
(Ⅲ)由题意得,G(3,4λ﹣1,0).
∴![]() ,
,
设平面AEG的法向量为![]() ,即
,即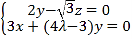 ,
,
令y=3,则![]() ,x=3﹣4λ,
,x=3﹣4λ,
∴![]() ,
,
容易得平面AED的法向量为![]() ,
,
故可得 ,
,
解得![]() ,
,
∴![]() ,∴|CG|=λ|CF|=4λ
,∴|CG|=λ|CF|=4λ![]() ,
,
∵|CG|≤4,
∴![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线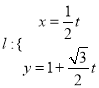 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)过点(1,
(a>b>0)过点(1,![]() ),过椭圆C的一个焦点作与长轴垂直的直线,被椭圆C截得的弦长为1
),过椭圆C的一个焦点作与长轴垂直的直线,被椭圆C截得的弦长为1
(1)求椭圆C的标准方程
(2)已知点P为椭圆C上不同于顶点的一点,A,B为椭圆C的左,右顶点,直线AP,BP分别与直线x=﹣6交于M,N两点设线段MN中点为Q,求![]() 的取最小值时点Q的坐标.
的取最小值时点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在两个成语中,一个成语的末字恰是另一成语的首字,则称这两个成语有顶真关系,现从分别贴有成语“人定胜天”、“争先恐后”、“一马当先”、“天马行空”、“先发制人”的5张大小形状完全相同卡片中,任意抽取2张,则这2张卡片上的成语有顶真关系的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为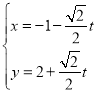 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标与参数方程
在直角坐标系![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).在以
为参数).在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系中,曲线
轴正半轴为极轴建立极坐标系中,曲线![]() :
: ![]() .
.
(1)当![]() ,
, ![]() 时,判断直线
时,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当![]() 时,若直线与曲
时,若直线与曲![]() 线
线![]() 相交于
相交于![]() ,
, ![]() 两点,设
两点,设![]() ,且
,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com