
【题目】已知扇形的圆心角是α,半径为R,弧长为l.
(1)若α=75°,R=12 cm,求扇形的弧长l和面积;
(2)若扇形的周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对定义域分别是![]() 、
、![]() 的函数
的函数![]() ,
,![]() ,一个函数
,一个函数![]() :
: .
.
(Ⅰ)若![]() ,
,![]() ,写出函数
,写出函数![]() 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() ,
,![]() 时,若函数
时,若函数![]() 有四个零点,分别为
有四个零点,分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
(1)请写出程序框图所表示的函数表达式;
(2)求输出的y(y<5)的概率;
(3)求输出的y(6<y≤8)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2﹣4x﹣5=0”的充分不必要条件
C.命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x≥﹣1,则x2﹣2x﹣3≤0”
D.已知命题 p:x∈R,x2+x﹣1<0,则p:x∈R,x2+x﹣1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则 ![]() 的最小值为( )
的最小值为( )
A.2
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 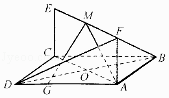
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com