
【题目】已知函数![]() 在
在![]() (
(![]() 为自然对数的底)时取得极值且有两个零点.
为自然对数的底)时取得极值且有两个零点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)记函数![]() 的两个零点为
的两个零点为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
试题分析:(1)由题意得![]() 可求
可求![]() ,再根据导函数零点确定函数单调性变化规律:函数
,再根据导函数零点确定函数单调性变化规律:函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,结合函数在端点处变化趋势,确定函数有两个零点的条件:
上递减,结合函数在端点处变化趋势,确定函数有两个零点的条件:![]() ,
,![]() (2)本题实质为极点偏移,先转化不等式:
(2)本题实质为极点偏移,先转化不等式:![]() 为
为![]() ,由
,由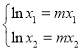 ,再转化为
,再转化为![]() ,由
,由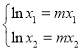 解得
解得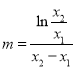 ,从而转化为
,从而转化为![]() ,即
,即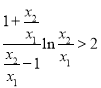 .令
.令![]() ,转化为
,转化为![]() ,然后构造函数
,然后构造函数![]() ,只需证明其最小值大于零.利用导数可得
,只需证明其最小值大于零.利用导数可得![]() 在
在![]() 单调递增,因此
单调递增,因此![]()
试题解析:(1)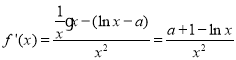 ,
,
由![]() ,且当
,且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 时取得极值,所以
时取得极值,所以![]() ,
,
所以![]() ,
,![]() ,
,![]() ,函数
,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,![]() ,
,
![]() 时
时![]() ;
;![]() 时,
时,![]() ,
,![]() 有两个零点
有两个零点![]() ,
,![]() ,
,
故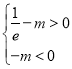 ,
,![]() ;
;
(2)不妨设![]() ,,由题意知
,,由题意知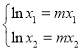 ,
,
则![]() ,
,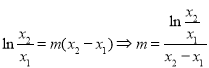 ,
,
欲证![]() ,只需证明:
,只需证明:![]() ,只需证明:
,只需证明:![]() ,
,
即证:![]() ,
,
即证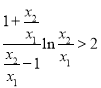 ,设
,设![]() ,则只需证明:
,则只需证明:![]() ,
,
也就是证明:![]() .
.
记![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,所以原不等式成立,故
,所以原不等式成立,故![]() 得证.
得证.


科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的![]() 三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产
三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产![]() 部件6件,或
部件6件,或![]() 部件3件,或
部件3件,或![]() 部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产
部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产![]() 部件的人数与生产
部件的人数与生产![]() 部件的人数成正比,比例系数为
部件的人数成正比,比例系数为![]() (
(![]() 为正整数).
为正整数).
(1)设生产![]() 部件的人数为
部件的人数为![]() ,分别写出完成
,分别写出完成![]() 三件部件生产需要的时间;
三件部件生产需要的时间;
(2)假设这三种部件的生产同时开工,若![]() ,求完成订单任务的最短时间,并给出此时具体的人数分组方案.
,求完成订单任务的最短时间,并给出此时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若ρ1=ρ2≠0,θ1+θ2=π,则点M1(ρ1,θ1)与点M2(ρ2,θ2)的位置关系是( )
A. 关于极轴所在的直线对称
B. 关于极点对称
C. 关于过极点垂直于极轴的直线对称
D. 重合
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①三点确定一个平面;②一条直线和一个点确定一个平面;③若四点不共面,则每三点一定不共线;④三条平行直线确定三个平面.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句中是命题的有( )
①空集是任何集合的真子集.
②3x-2>0.
③垂直于同一条直线的两条直线必平行吗?
④把门关上.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l与l1关于点(1,-1)成中心对称,若l的方程是2x+3y-6=0,则l1的方程是( )
A. 2x+3y+8=0 B. 2x+3y+7=0
C. 3x-2y-12=0 D. 3x-2y+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2≥4},B={m}.若A∪B=A,则m的取值范围是( )
A. (-∞,-2) B. [2,+∞)
C. [-2,2] D. (-∞,-2]∪[2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com