
 、
、 都是单位向量,则
都是单位向量,则 ;
; ;
; 、
、 与
与 是三个非零向量,则
是三个非零向量,则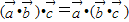 ;
; 与
与 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得 成立.
成立. ,但是不一定有
,但是不一定有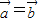 ,故不正确;
,故不正确; ,k∈Z},故合在一起即为{α|
,k∈Z},故合在一起即为{α| ,n∈Z},故②正确;
,n∈Z},故②正确; 、
、 与
与 是三个非零向量,∴
是三个非零向量,∴ 与
与 不一定共线,故
不一定共线,故 不一定成立,因此③不正确;
不一定成立,因此③不正确; (k∈Z)上单调递增,但是在整个定义域上不单调,故④不正确;
(k∈Z)上单调递增,但是在整个定义域上不单调,故④不正确; 与
与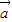 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得 成立,而不是使得
成立,而不是使得 成立,故不正确.
成立,故不正确.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| x2+2x-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:022
有下列四个命题:
A.“a,b都是正数”的否定形式是“a,b都不是正数”;
B.若x∈R,则|x|≥x;
C.单元素集不是空集;
D.“明天刮风下雨”是复合命题“p且q”的形式,
其中真命题是________(填命题的序号).
查看答案和解析>>
科目:高中数学 来源:2011年江苏省如皋市高一上学期期中考试数学 题型:填空题
下列命题正确的个数为__ ▲ ___
①若 ,则函数
,则函数 的图象不经过第三象限;
的图象不经过第三象限;
②已知函数 定义域是
定义域是 ,则
,则 的定义域是
的定义域是 ;
;
③函数 的单调减区间是
的单调减区间是
④已知集合 ,那么
,那么 ;
;
⑤已知函数 是定义在
是定义在 上的不恒为
上的不恒为 的函数,且对于任意的
的函数,且对于任意的 ,都有
,都有 ,则函数
,则函数 为奇函数.
为奇函数.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x2+2x-3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南通市如皋市高一(上)期中数学试卷(解析版) 题型:填空题
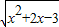 的单调减区间是(-∞,-1)
的单调减区间是(-∞,-1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com