
| 2 |
| A、x2+y2-x-2y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2-2=0 |
| D、x2+y2-1=0 |
| 2 |
|a-2a+
| ||
|
(
| ||
| 2 |
| 2 |
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
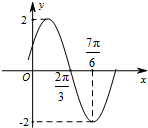 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
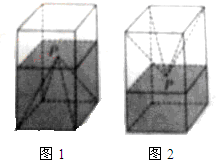 如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题:
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com