[题目]已知抛物线y2=4x的焦点F.过焦点的直线与抛物线交于A.B两点.则4|FA|+|FB|的最小值为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知抛物线y2=4x的焦点F，过焦点的直线与抛物线交于A，B两点，则4|FA|+|FB|的最小值为．

【答案】9
【解析】解：抛物线的焦点为F（1，0），（1）若直线与x轴垂直，则直线方程为x=1，

代入抛物线方程得y=±2，

∴|FA|=|FB|=2，

∴4|FA|+|FB|=10．（2）若直线与x轴不垂直，显然直线有斜率，

设直线方程为y=k（x﹣1），

联立方程组，消元得k2x2﹣（2k2+4）x+k2=0，

设A（x1，y1），B（x2，y2），

则x1x2=1，即x2= ，

∵A，B在抛物线上，∴|FA|=x1+1，|FB|=x2+1= ，

∴4|FA|+|FB|=4x1+4+ +1=4x1+ +5≥2 +5=9．

当且仅当4x1= 即x1= 时取等号．

综上，4|FA|+|FB|的最小值为9．

所以答案是：9．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy中，圆C的参数方程（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C的极坐标方程；
（2）直线l的极坐标方程是2ρsin（θ+ ）=3 ，射线OM：θ= 与圆C的交点为O、P，与直线l的交点为Q，求线段PQ的长．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图直三棱柱ABC﹣A1B1C1 中AC=2AA1 ， AC⊥BC，D、E 分别为A1C1、AB 的中点．求证：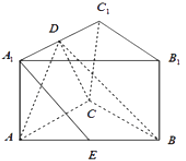

（1）AD⊥平面BCD
（2）A1E∥平面BCD．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在边长为2的正三角形△ABC中，D为BC的中点，E，F分别在边CA，AB上．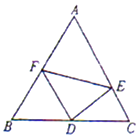
（1）若，求CE的长；
（2）若∠EDF=60°，问：当∠CDE取何值时，△DEF的面积最小？并求出面积的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】我国南宋时期的数学家秦九韶是普州（现四川省安岳县）人，秦九韶在其所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一例，则输出的S的值为（）
A.4
B.﹣5
C.14
D.﹣23

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）=ex+sinx（e为自然对数的底数），g（x）=ax，F（x）=f（x）﹣g（x）．
（1）若x=0是F（x）的极值点，且直线x=t（t≥0）分别与函数f（x）和g（x）的图象交于P，Q，求P，Q两点间的最短距离；
（2）若x≥0时，函数y=F（x）的图象恒在y=F（﹣x）的图象上方，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在△ABC中，sin = ，AB=2，点D在线段AC上，且AD=2DC，BD= ，则cosC= ．