
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 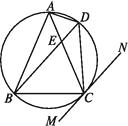
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
【答案】
(1)证明:∵BD∥MN,∴∠CDB=∠DCN.
又∠BAE=∠CDB,
∴∠BAE=∠DCN.
又直线MN是☉O的切线,
∴∠DCN=∠CAD.
∴∠BAE=∠CAD.
又∠ABE=∠ACD,AB=AC,
∴△ABE≌△ACD.
(2)证明:∵∠EBC=∠BCM,∠BCM=∠BDC,
∴∠EBC=∠BDC.
∴CB=CD.
∵∠BEC=∠EDC+∠ECD,∠ECD=∠ABE,
∴∠BEC=∠EBC+∠ABE=∠ABC.
又AB=AC,
∴∠ABC=∠ECB.
∴∠BEC=∠ECB.
∴BE=BC.
【解析】本题主要考查了弦切角的性质,解决问题的关键是根据弦切角的性质(1)由已知,得∠ABE=∠ACD,只需证明∠BAE=∠CAD,转化为证明∠BAE=∠CDB,∠CDB=∠DCN,∠DCN=∠CAD.(2)转化为证明∠BEC=∠ECB.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法: ①线性回归分析就是由样本点去寻找一条直线,使之贴近这些样本点的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归方程 ![]() ,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验.其中正确命题的个数是( )
,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验.其中正确命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 函数f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的图象关于原点对称,其中m,n为实常数.
(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[﹣2,2]上是单调函数;
(3)当﹣2≤x≤2 时,不等式f(x)≥(n﹣logma)logma恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +m为奇函数,m为常数.
+m为奇函数,m为常数.
(1)求实数m的值;
(2)判断并证明f(x)的单调性;
(3)若关于x的不等式f(f(x))+f(ma)<0有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com