
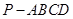 中,底面
中,底面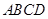 是矩形,
是矩形,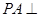 平面
平面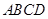 ,
,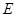 、
、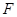 分别是
分别是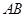 、
、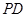 的中点.
的中点.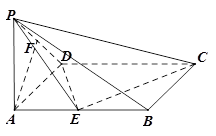
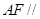 平面
平面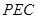 ;
;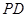 与平面
与平面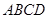 所成角为
所成角为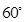 ,且
,且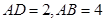 ,求点
,求点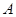 到平面
到平面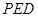 的距离.
的距离. .
.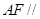 平面
平面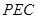 ,关键是在平面
,关键是在平面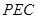 内找到一条与直线
内找到一条与直线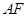 平行的直线,本题就想是否有一个过直线
平行的直线,本题就想是否有一个过直线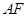 的平面与平面
的平面与平面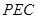 相交,交线就是我们要找的平行直线(可根据线面平行的性质定理知),在图形中可容易看出应该就是平面
相交,交线就是我们要找的平行直线(可根据线面平行的性质定理知),在图形中可容易看出应该就是平面 ,只不过再想一下,交线到底是什么而已,当然具体辅助线的作法也可换成另一种说法(即试题解析中的直接取
,只不过再想一下,交线到底是什么而已,当然具体辅助线的作法也可换成另一种说法(即试题解析中的直接取 中点
中点 ,然后连接
,然后连接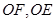 的方法);(2)由于
的方法);(2)由于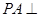 平面
平面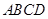 ,所以三棱锥
,所以三棱锥 的体积可以很快求出,从而本题可用体积法求点
的体积可以很快求出,从而本题可用体积法求点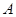 到平面
到平面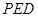 的距离,另外由于
的距离,另外由于 ,如果取
,如果取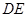 中点
中点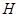 ,则有
,则有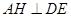 ,从而可得
,从而可得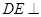 平面
平面 ,也即平面
,也即平面
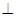 平面
平面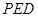 ,这时点
,这时点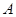 到平面
到平面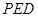 的垂线段可很快作出,从而迅速求出结论.
的垂线段可很快作出,从而迅速求出结论. 的中点
的中点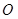 ,连接
,连接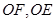 .
.
 且
且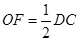 ,
, 是
是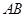 的中点,则
的中点,则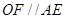 且
且 ,
,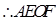 是平行四边形, ∴
是平行四边形, ∴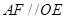
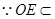 平面
平面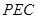 ,
,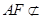 平面
平面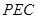
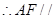 平面
平面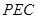
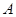 平面
平面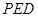 的距离为
的距离为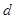 ,
,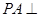 平面
平面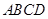 ,故
,故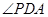 为
为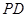 与平面
与平面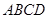 所成角,所以
所成角,所以 ,
, ,
,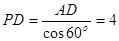 ,又因
,又因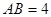 ,
,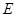 是
是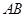 的中点所以
的中点所以 ,
, ,
, .
. 于
于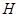 ,因
,因 ,则
,则 ,
,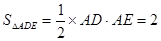 ,
,
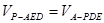 所以
所以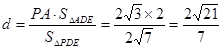
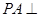 平面
平面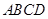 ,故
,故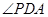 为
为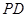 与平面
与平面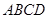 所成角,所以
所成角,所以 ,
, ,
,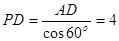 ,又因
,又因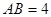 ,
,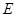 是
是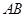 的中点所以
的中点所以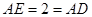 ,
, ,
, .
. 于
于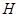 ,连结
,连结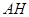 ,因
,因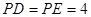 ,则
,则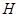 为
为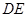 的中点,故
的中点,故
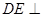 平面
平面 ,所以平面
,所以平面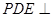 平面
平面 ,作
,作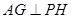 于
于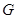 ,则
,则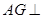 平面
平面 ,所以线段
,所以线段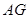 的长为
的长为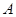 平面
平面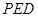 的距离.
的距离. ,
,
 .
.

科目:高中数学 来源:不详 题型:单选题
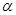 和
和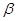 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: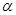 外一条直线
外一条直线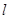 与
与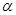 内一条直线平行,则
内一条直线平行,则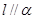 ;
;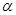 内两条相交直线分别平行于
内两条相交直线分别平行于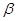 内的两条直线 ,则
内的两条直线 ,则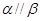 ;
;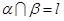 ,若
,若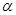 内有一条直线垂直于
内有一条直线垂直于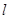 ,则
,则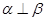 ;
;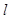 与平面
与平面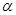 内的无数条直线垂直,则
内的无数条直线垂直,则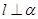 .
.| A.①③ | B.②④ | C.①② | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是空间两条直线,
是空间两条直线,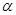 ,
,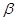 是空间两个平面,则下列选项中不正确的是( )
是空间两个平面,则下列选项中不正确的是( )A.当 时,“ 时,“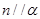 ”是“ ”是“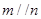 ”的必要不充分条件 ”的必要不充分条件 |
B.当 时,“ 时,“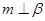 ”是“ ”是“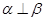 ”的充分不必要条件 ”的充分不必要条件 |
C.当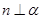 时, “ 时, “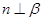 ”是“ ”是“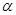 ∥ ∥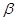 ”成立的充要条件 ”成立的充要条件 |
D.当 时,“ 时,“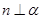 ”是“ ”是“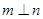 ”的充分不必要条件 ”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com