
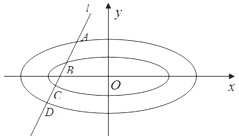
 已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).
已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).分析 (Ⅰ)设椭圆C1的焦距为2c1,长轴为2a1,短轴为2b1,设椭圆C2的焦距为2c2,长轴为2a2,短轴为2b2,
利用已知条件,求出两个椭圆的几何量,得到椭圆的方程.
(Ⅱ)|AC|=|BD|,①当直线l的斜率不存在时,显然有|AC|=|BD|.②当直线l的斜率存在时,设直线l的方程为y=kx+m,设点A坐标为(x1,y1),点B坐标为(x2,y2),点C坐标为(x3,y3),点D坐标为(x4,y4),联立直线与椭圆方程,通过韦达定理线段的中点是否相同.证明即可.
解答 (本小题满分14分)
解:(Ⅰ)设椭圆C1的焦距为2c1,长轴为2a1,短轴为2b1,设椭圆C2的焦距为2c2,长轴为2a2,短轴为2b2,
依题意得$\left\{\begin{array}{l}\frac{c_1}{a_1}=\frac{{\sqrt{2}}}{2}\\{c_1}=1\\{a_1}^2={b_1}^2+{c_1}^2\end{array}\right.$,$\left\{\begin{array}{l}\frac{c_2}{a_2}=\frac{{\sqrt{2}}}{2}\\{a_2}=2\\{a_2}^2={b_2}^2+{c_2}^2\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a_1}=\sqrt{2}\\{b_1}=1\end{array}\right.$,$\left\{\begin{array}{l}{a_2}=2\\{b_2}=\sqrt{2}\end{array}\right.$,
所以椭圆C1的标准方程为$\frac{x^2}{2}+{y^2}=1$,
所以椭圆C2的标准方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.….(4分)
(Ⅱ)|AC|=|BD|.….(5分)
①当直线l的斜率不存在时,显然有|AC|=|BD|.….(6分)
②当直线l的斜率存在时,设直线l的方程为y=kx+m,
设点A坐标为(x1,y1),点B坐标为(x2,y2),
点C坐标为(x3,y3),点D坐标为(x4,y4),
将直线l的方程与椭圆C1方程联立可得$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,.….(8分)
消去y得(1+2k2)x2+4kmx+2m2-2=0,
所以有${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}$,.….(9分)
将直线l的方程与椭圆C2方程联立可得$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$,
消去y得(1+2k2)x2+4kmx+2m2-4=0,
所以有${x_1}+{x_2}=-\frac{4km}{{1+2{k^2}}}$,.….(11分)
所以有弦AD的中点与弦BC的中点重合,.….(13分)
所以有|AC|=|BD|.….(14分)
点评 本题考查直线与椭圆方程的综合应用,椭圆方程的求法,考查转化思想以及计算能力.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | -4 | C. | -$\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | $(\frac{3}{2},+∞)$ | C. | (-3,1)∪$(\frac{3}{2},+∞)$ | D. | $(-3,\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
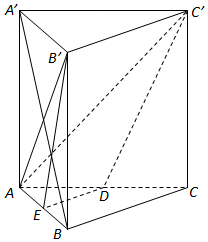 如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.
如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com