
【题目】![]() 满足约束条件
满足约束条件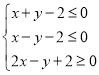 ,若
,若![]() 取得最大值的最优解不唯一,则实数a的值为( )
取得最大值的最优解不唯一,则实数a的值为( )
A.![]() 或-1B.2或
或-1B.2或![]() C.2或1D.2或-1
C.2或1D.2或-1
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】下列四个结论:
![]() 两条直线和同一个平面垂直,则这两条直线平行;
两条直线和同一个平面垂直,则这两条直线平行;
![]() 两条直线没有公共点,则这两条直线平行;
两条直线没有公共点,则这两条直线平行;
![]() 两条直线都和第三条直线垂直,则这两条直线平行;
两条直线都和第三条直线垂直,则这两条直线平行;
![]() 一条直线和一个平面内任意直线没有公共点,则这条直线和这个平面平行.
一条直线和一个平面内任意直线没有公共点,则这条直线和这个平面平行.
其中正确的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与两个定点
与两个定点![]() 距离的比是一个正数
距离的比是一个正数![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)当![]() 时得曲线
时得曲线![]() 的方程,把曲线
的方程,把曲线![]() 向左平移三个单位长度得到曲线
向左平移三个单位长度得到曲线![]() ,已知点
,已知点![]() ,
,![]() ,点
,点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值;
的最小值;
(3)若直线![]() 与曲线
与曲线![]() 交于C、D两点,点
交于C、D两点,点![]() 是x轴上的点,使得
是x轴上的点,使得![]() 恒为定值,求点P的坐标和定值.
恒为定值,求点P的坐标和定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(1)根据已知数据,把表格数据填写完整;
(2)若在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,求从这5人中随机抽取3人至多有1人是教师的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com