
【题目】求符合下列条件的直线方程:
(1)过点![]() ,且与直线
,且与直线![]() 平行;
平行;
(2)过点![]() ,且与直线
,且与直线![]() 垂直;
垂直;
(3)过点![]() ,且在两坐标轴上的截距相等.
,且在两坐标轴上的截距相等.
科目:高中数学 来源: 题型:
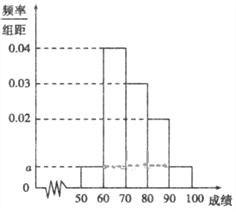
【题目】某校![]() 名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:
名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1).求图中![]() 的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
的值; 并根据频率分布直方图,估计这100名学生语文成绩的平均分;
(2).若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如上右表所示,求数学成绩在
)之比如上右表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程:![]() 和直线l的方程:
和直线l的方程:![]() ,点P是圆C上动点,直线l与两坐标轴交于A、B两点.
,点P是圆C上动点,直线l与两坐标轴交于A、B两点.
(1)求与圆C相切且垂直于直线l的直线方程;
(2)求![]() 面积的取值范围。
面积的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某市2017年2月28天的日空气质量指数折线图.
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅰ)请根据所给的折线图补全如图2所示的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲,乙两种产品均需用![]() 两种原料,已知生产1吨每种产品需用
两种原料,已知生产1吨每种产品需用![]() 原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击![]() 次,至少击中
次,至少击中![]() 次的概率:先由计算机给出
次的概率:先由计算机给出![]() 到
到![]() 之间取整数值的随机数,指定
之间取整数值的随机数,指定![]() ,
,![]() 表示没有击中目标,
表示没有击中目标,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示击中目标,以
表示击中目标,以![]() 个随机数为一组,代表射击
个随机数为一组,代表射击![]() 次的结果,经随机模拟产生了
次的结果,经随机模拟产生了![]() 组随机数:
组随机数:
![]()
根据以上数据统计该运动员射击![]() 次至少击中
次至少击中![]() 次的概率为( )
次的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:对数 ![]() 有意义;命题q:实数t满足不等式
有意义;命题q:实数t满足不等式 ![]() .(Ⅰ)若命题p为真,求实数
.(Ⅰ)若命题p为真,求实数 ![]() 的取值范围;
的取值范围;
(Ⅱ)若命题p是命题q的充分不必要条件,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某初级中学有三个年级,各年级男、女人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 |
| 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求 ![]() 的值;
的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,求该样本中女生的人数;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2,1.5,1.2,1.5,1.5,1.3,1.0,1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com