
【题目】如图,直角梯形ABCD与等边△ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=AD=2,F为线段EA上的点,且EA=3EF. 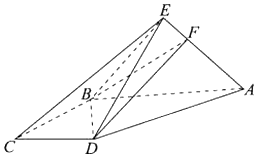
(I)求证:EC∥平面FBD
(Ⅱ)求多面体EFBCD的体积.
【答案】解:(Ⅰ)连接AC、BD交于点O,连接FO,
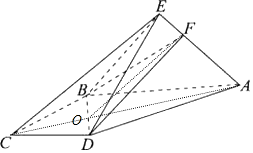
在梯形ABCD中,有△DOC与△BOA相似,可得OA=2OC,AC=3OC,
又EA=3EF,∴FO∥EC
又FO面FBD,EC面FBD
平面ACE∩平面FBD=FM.
∴EC∥平面FBD;
(Ⅱ)多面体EFBCD的体积V=VE﹣ABCD﹣VF﹣ABD
= ![]() ×
× ![]() =
= ![]() .
.
【解析】(Ⅰ)连接AC、BD交于点O,连接FO,可得AC=3OC,又EA=3EF,得FO∥EC即可证得EC∥平面FBD (Ⅱ)多面体EFBCD的体积V=VE﹣ABCD﹣VF﹣ABD= ![]() ×
× ![]() =
= ![]()
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)=a﹣x2( ![]() ≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
A.[1, ![]() +2]
+2]
B.[1,e2﹣2]
C.[ ![]() +2,e2﹣2]
+2,e2﹣2]
D.[e2﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为;若采用分层抽样,40﹣50岁年龄段应抽取人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,函数f(x)=2cosxsin(x﹣A)+sinA(x∈R)在x= ![]() 处取得最大值.
处取得最大值.
(1)当 ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣1,1),且同时满足下列条件:
①f(x)是奇函数;
②f(x)在定义域上单调递减;
③f(1﹣a)+f(1﹣a2)<0.
求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=1,且an+1=2an+1(n∈N*)
(Ⅰ)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Sn;
,求数列{bn}的前n项和Sn;
(Ⅲ)在条件(Ⅱ)下对任意正整数n,不等式Sn+ ![]() ﹣1>(﹣1)na恒成立,求实数a的取值范围.
﹣1>(﹣1)na恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,则( )
)的部分图象如图所示,则( )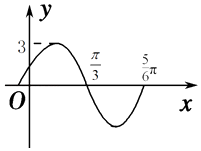
A.f(x)的一个对称中心为 ![]()
B.f(x)的图象关于直线 ![]() 对称
对称
C.f(x)在 ![]() 上是增函数
上是增函数
D.f(x)的周期为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com