
【题目】综合题。
(1)证明:Cnm+Cnm﹣1=Cn+1m;
(2)证明:Cn1+2Cn2+3Cn3+…+nCnn=n2n﹣1 .
【答案】
(1)证明:三种方法:法一:直接代公式:Cnm+Cnm﹣1= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
又Cn+1m= ![]() ,∴Cnm+Cnm﹣1=Cn+1m.
,∴Cnm+Cnm﹣1=Cn+1m.
法二:(构造)从一个装有n个不同的红球和1个黄球的口袋中取出m个不同球,共得到 ![]() 个不同组合,我们可将这些组合分成两类:一类全是红球,则从n个红球中取,可得到
个不同组合,我们可将这些组合分成两类:一类全是红球,则从n个红球中取,可得到 ![]() 个不同组合;一类含有黄球,则从n个红球中再取出m﹣1个,则得到
个不同组合;一类含有黄球,则从n个红球中再取出m﹣1个,则得到 ![]() 个不同组合,所以
个不同组合,所以 ![]() .
.
法三(构造)分别求(1+x)n+1和(1+x)(1+x)n的展开式中xm的系数,
(1+x)n+1的展开式中xm的系数为 ![]() ;
;
(1+x)(1+x)n=(1+x)( ![]() )的展开式中xm的系数为1×
)的展开式中xm的系数为1× ![]() +1×
+1× ![]() =
= ![]() +
+ ![]() ,
,
∵(1+x)n+1=(1+x)(1+x)n,∴展开式中xm的系数也相等,∴ ![]()
(2)证明:法一:倒序相加法:f(n)=Cn1+2Cn2+3Cn3+…+nCnn,f(n)=nCnn+(n﹣1) ![]() …+3Cn3+2Cn2+Cn1,∴2f(n)=nCnn+(n﹣1+1)
…+3Cn3+2Cn2+Cn1,∴2f(n)=nCnn+(n﹣1+1) ![]() +…+(1+n﹣1)
+…+(1+n﹣1) ![]() +n
+n ![]()
=n( ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() )=n2n,∴f(n)=n2n﹣1.
)=n2n,∴f(n)=n2n﹣1.
法二:公式法:利用公式 ![]() ,则Cn1+2Cn2+3Cn3+…+nCnn=n
,则Cn1+2Cn2+3Cn3+…+nCnn=n ![]() +n
+n ![]() +…+n
+…+n ![]() =n(
=n( ![]() +
+ ![]() +…+
+…+ ![]() )=n2n﹣1,
)=n2n﹣1,
∴Cn1+2Cn2+3Cn3+…+nCnn=n2n﹣1.
法三:构造函数f (x)=(1+x)n= ![]() ,两边求导得:
,两边求导得: ![]()
令x=1得: ![]() 成立
成立
【解析】(1)三种方法:法一:直接利用组合数的计算公式即可证明. 法二:(构造)从一个装有n个不同的红球和1个黄球的口袋中取出m个不同球,共得到 ![]() 个不同组合,我们可将这些组合分成两类:一类全是红球,则从n个红球中取m个不同的球;一类含有黄球,则从n个红球中再取出m﹣1个,即可得出.法三(构造)分别求(1+x)n+1和(1+x)(1+x)n的展开式中xm的系数,利用二项式定理的展开式即可得出.(2)法一:倒序相加法;法二:公式法:利用公式
个不同组合,我们可将这些组合分成两类:一类全是红球,则从n个红球中取m个不同的球;一类含有黄球,则从n个红球中再取出m﹣1个,即可得出.法三(构造)分别求(1+x)n+1和(1+x)(1+x)n的展开式中xm的系数,利用二项式定理的展开式即可得出.(2)法一:倒序相加法;法二:公式法:利用公式 ![]() 和
和 ![]() ,即可证明.法三:构造函数f (x)=(1+x)n=
,即可证明.法三:构造函数f (x)=(1+x)n= ![]() ,两边求导得:令x=1即可证明.
,两边求导得:令x=1即可证明.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
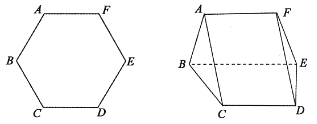
【题目】如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且![]() ,(1)证明:平面ABEF
,(1)证明:平面ABEF![]() 平面BCDE; (2)求DE与平面ABC所成角的正弦值。
平面BCDE; (2)求DE与平面ABC所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知(x+ ![]() )n展开式的二项式系数之和为256
)n展开式的二项式系数之和为256
(1)求n;
(2)若展开式中常数项为 ![]() ,求m的值;
,求m的值;
(3)若展开式中系数最大项只有第6项和第7项,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批有10个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽取到的可能性相同.在下列三种情况下,分别求出直到取出合格品为止时所需抽取次数x的分布列.
(1)每次取出的产品都不放回此批产品中;
(2)每次取出的产品都立即放回此批产品中,然后再取出一件产品;
(3)每次取出一件产品后总以一件合格品放回此批产品中.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:“存在 ![]() ”,命题q:“曲线
”,命题q:“曲线 ![]() 表示焦点在x轴上的椭圆”,命题s:“曲线
表示焦点在x轴上的椭圆”,命题s:“曲线 ![]() 表示双曲线”
表示双曲线”
(1)若“p且q”是真命题,求m的取值范围;
(2)若q是s的必要不充分条件,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com