
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
分析 由于点P到y轴的距离比点P到焦点的距离小$\frac{1}{2}$,故可转化为点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与到焦点的距离之和的最小值来求.
解答 解:抛物线y2=2x的焦点F的坐标为($\frac{1}{2}$,0)
过点D$(2,\frac{3}{2}\sqrt{3})$和抛物线焦点的直线和抛物线的上半部分交于点A,
由于点P到y轴的距离比点P到焦点的距离小$\frac{1}{2}$,
故可以根据点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与到焦点的距离之和的最小值来求,
根据三角形两边之和大于第三边知|PD|+|PF|>|DF|=3(可以取到等号,此时P和A重合),
故点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与到y轴的距离之和的最小值为3-$\frac{1}{2}$=$\frac{5}{2}$,
故选:B
点评 本题考查的知识点抛物线的简单性质,熟练掌握抛物线的性质,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$$\sqrt{3}$ | B. | 3 | C. | 8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | (1,2] | C. | ($\frac{1}{2}$,2] | D. | [$\frac{1}{2}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | T3 | B. | T4 | C. | T5 | D. | T6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x3<0 | |
| B. | 在斜二测画法中,直观图的面积是原图形面积的4$\sqrt{2}$ | |
| C. | “a>0”是“|a|>0”充分不必要的条件 | |
| D. | 关于x的不等式x2-2ax-8a2<0(a>0)的解集为(x1,x2),且x2-x1=15,则$a=\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
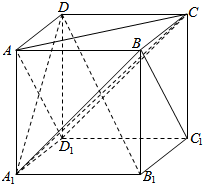 如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com