
【题目】已知函数![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 恰有一个零点,求
恰有一个零点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 或
或![]() (2)
(2) ![]()
【解析】【试题分析】(1)函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() ,对
,对![]() 分类讨论,得到函数的单调区间,由此求得
分类讨论,得到函数的单调区间,由此求得![]() 的取值范围.(2) 令
的取值范围.(2) 令![]() ,利用
,利用![]() 的导数,对
的导数,对![]() 分类讨论函数的单调区间,利用最大值小于零,来求得
分类讨论函数的单调区间,利用最大值小于零,来求得![]() 的取值范围.
的取值范围.
【试题解析】
(1)函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
①当![]() 时,
时, ![]() 时无零点,
时无零点,
②当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
取![]() ,则
,则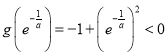 ,
,
因为![]() ,所以
,所以![]() ,此时函数
,此时函数![]() 恰有一个零点,
恰有一个零点,
③当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在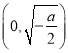 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在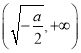 上单调递增.
上单调递增.
要使函数![]() 有一个零点,则
有一个零点,则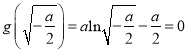 即
即![]() ,
,
综上所述,若函数![]() 恰有一个零点,则
恰有一个零点,则![]() 或
或![]() ;
;
(2)令![]() ,根据题意,当
,根据题意,当![]() 时,
时, ![]() 恒成立,又
恒成立,又![]() ,
,
①若![]() ,则
,则![]() 时,
时, ![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符题意.
,所以不符题意.
②若![]() ,则
,则![]() 时,
时, ![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以不符题意.
,所以不符题意.
③若![]() ,则
,则![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,于是“
上是减函数,于是“![]() 对任意
对任意![]() ,都成立”的充要条件是
,都成立”的充要条件是![]() ,即
,即![]() ,解得
,解得![]() ,故
,故![]() .
.
综上, ![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过调查得到如下数据:
之间的关系,经过调查得到如下数据:
间隔时间/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值都不超过
的差,若差值的绝对值都不超过![]() ,则称所求方程是“恰当回归方程”.
,则称所求方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取2组数据,求选取的这
组数据中随机选取2组数据,求选取的这![]() 组数据的间隔时间不相邻的概率;
组数据的间隔时间不相邻的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
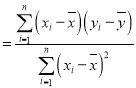 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
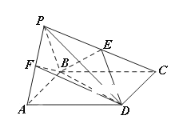
【题目】如图,四棱锥![]() 中,
中,![]() 是正三角形,四边形ABCD是矩形,且平面
是正三角形,四边形ABCD是矩形,且平面![]() 平面
平面![]() .
.
(1)若点E是PC的中点,求证:![]() 平面BDE;
平面BDE;
(2)若点F在线段PA上,且![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() 时,求实数
时,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,斜率为正的直线l过点F交抛物线于A、B两点,满足
的焦点为F,斜率为正的直线l过点F交抛物线于A、B两点,满足![]() .
.
(1)求直线l的斜率;
(2)设点![]() 在线段
在线段![]() 上运动,原点
上运动,原点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺公司要对某种工艺品深加工,已知每个工艺品进价为20元,每个的加工费为n元,销售单价为x元.根据市场调查,须有![]() ,
,![]() ,
,![]() ,同时日销售量m(单位:个)与
,同时日销售量m(单位:个)与![]() 成正比.当每个工艺品的销售单价为29元时,日销售量为1000个.
成正比.当每个工艺品的销售单价为29元时,日销售量为1000个.
(1)写出日销售利润y(单位:元)与x的函数关系式;
(2)当每个工艺品的加工费用为5元时,要使该公司的日销售利润为100万元,试确定销售单价x的值.(提示:函数![]() 与
与![]() 的图象在
的图象在![]() 上有且只有一个公共点)
上有且只有一个公共点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场在2018年国庆举办了一次抽奖活动抽奖箱里放有3个红球,3个黑球和1个白球![]() 这些小球除颜色外大小形状完全相同
这些小球除颜色外大小形状完全相同![]() ,从中随机一次性取3个小球,每位顾客每次抽完奖后将球放回抽奖箱活动另附说明如下:
,从中随机一次性取3个小球,每位顾客每次抽完奖后将球放回抽奖箱活动另附说明如下:
![]() 凡购物满
凡购物满![]() 含
含![]() 元者,凭购物打印凭条可获得一次抽奖机会;
元者,凭购物打印凭条可获得一次抽奖机会;
![]() 凡购物满
凡购物满![]() 含
含![]() 元者,凭购物打印凭条可获得两次抽奖机会;
元者,凭购物打印凭条可获得两次抽奖机会;
![]() 若取得的3个小球只有1种颜色,则该顾客中得一等奖,奖金是一个10元的红包;
若取得的3个小球只有1种颜色,则该顾客中得一等奖,奖金是一个10元的红包;
![]() 若取得的3个小球有3种颜色,则该顾客中得二等奖,奖金是一个5元的红包;
若取得的3个小球有3种颜色,则该顾客中得二等奖,奖金是一个5元的红包;
![]() 若取得的3个小球只有2种颜色,则该顾客中得三等奖,奖金是一个2元的红包.
若取得的3个小球只有2种颜色,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据![]() 单位:元
单位:元![]() ,绘制得到如图所示的茎叶图.
,绘制得到如图所示的茎叶图.

![]() 求这20位顾客中获得抽奖机会的顾客的购物消费数据的中位数与平均数
求这20位顾客中获得抽奖机会的顾客的购物消费数据的中位数与平均数![]() 结果精确到整数部分
结果精确到整数部分![]() ;
;
![]() 记一次抽奖获得的红包奖金数
记一次抽奖获得的红包奖金数![]() 单位:元
单位:元![]() 为X,求X的分布列及数学期望,并计算这20位顾客在抽奖中获得红包的总奖金数的平均值
为X,求X的分布列及数学期望,并计算这20位顾客在抽奖中获得红包的总奖金数的平均值![]() 假定每位获得抽奖机会的顾客都会去抽奖
假定每位获得抽奖机会的顾客都会去抽奖![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com