
已知函数f(x)=4x+m·2x+1有且仅有一个零点,求m的取值范围,并求出该零点.
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:解答题
某工厂生产某种产品,每日的成本C(单位:元)与日产量x(单位:吨)满足函数关系式C=10000+20x,每日的销售额R(单位:元)与日产量x满足函数关系式R=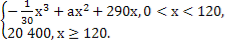
已知每日的利润y=R-C,且当x=30时,y=-100.
(1)求a的值.
(2)求当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:解答题
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直线m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边都在第一象限内,并且分别与单位圆相交于A,B两点,已知A点的纵坐标为 ,B点的纵坐标为
,B点的纵坐标为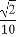 ,则tanα= ,tanβ= .
,则tanα= ,tanβ= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:选择题
已知扇形的面积为2cm2,扇形圆心角θ的弧度数是4,则扇形的周长为( )
(A)2cm (B)4cm (C)6cm (D)8cm
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:填空题
若函数f(x)=ax-x-a(a>0且a≠1)有两个零点,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
函数f(x)=|x-2|-lnx在定义域内零点的个数为( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:填空题
在平面直角坐标系内,点P(a,b)的坐标满足a≠b,且a,b都是集合{1,2,3,4,5,6}中的元素,又点P到原点的距离|OP|≥5.则这样的点P的个数为_______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十八第十章第五节练习卷(解析版) 题型:选择题
把一枚骰子投掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量p=(m,n),q=(-2,1),则p⊥q的概率为( )
(A)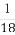 (B)
(B)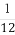 (C)
(C) (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com