
【题目】已知函数f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x﹣1,x∈R,若函数k(x)=f(x+a)的图象关于点(﹣
cos2x﹣1,x∈R,若函数k(x)=f(x+a)的图象关于点(﹣ ![]() ,0)对称,且α∈(0,π),则α=( )
,0)对称,且α∈(0,π),则α=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:∵f(x)=1﹣cos( ![]() +2x)﹣
+2x)﹣ ![]() cos2x﹣1
cos2x﹣1
=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() ),
),
∴h(x)=f(x+α)=2sin(2x+2α﹣ ![]() ),
),
∵其图象关于(﹣ ![]() ,0)对称,
,0)对称,
∴2×(﹣ ![]() )+2α﹣
)+2α﹣ ![]() =kπ,k∈Z,
=kπ,k∈Z,
∴2α=(k+1)π,k∈Z.
∴α= ![]() π,又α∈(0,π),
π,又α∈(0,π),
∴α= ![]() .
.
故选B.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂第一季度某产品月生产量分别为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量y (单位:万件)与月份x 的关系.模拟函数1:y=ax+ ![]() +c
+c
;模拟函数2:y=mnx+s.
(1)已知4月份的产量为13.7 万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高三年级的学生进行体检,现将高三男生体重(单位:kg)的数据进行整理后分为五组,并绘制出频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65 kg属于偏胖,低于55 kg属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25,0.20,0.10,0.05,第二小组的频数为400,则该校高三年级男生的总数和体重正常的频率分别为( )

A. 1000,0.50 B. 800,0.50
C. 800,0.60 D. 1000,0.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司经营一批进价为每件400元的商品,在市场调查时发现,此商品的销售单价x(元)与日销售量y(件)之间的关系如下表所示:
x/元 | 500 | 600 | 700 | 800 | 900 |
y/件 | 10 | 8 | 9 | 6 | 1 |
(1)求y关于x的回归直线方程.
(2)借助回归直线方程,预测销售单价为多少元时,日利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为![]() 立方米,且
立方米,且![]() .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为![]() (
(![]() )千元.设该容器的建造费用为
)千元.设该容器的建造费用为![]() 千元.
千元.
(1)写出![]() 关于
关于![]() 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() )的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
)的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出两个命题:
命题甲:关于x的不等式x2+(a﹣1)x+a2≤0的解集为;
命题乙:函数y=(2a2﹣a)x为增函数.
(1)甲、乙至少有一个是真命题;
(2)甲、乙有且只有一个是真命题;
分别求出符合(1)(2)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2)
=1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2) 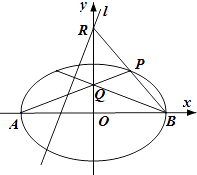
(1)求椭圆C的标准方程;
(2)求证: ![]() 为定值;
为定值;
(3)求证:过点R且与直线QB垂直的直线经过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com