
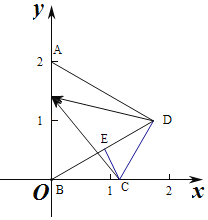
【题目】在平面四边形ABCD中,AB⊥BC,∠BCD=120°,△ABD是边长为2的正三角形,E是AB边上的动点,则![]()
![]() 的最小值为_____.
的最小值为_____.
【答案】![]()
【解析】
将四边形放入坐标系,结合三角函数定义求出对应点的坐标,利用向量数量积公式转化为一元二次函数进行求求解即可.
解:当四边形ABCD放入平面直角坐标系,
∵AB⊥BC,∠BCD=120°,△ABD是边长为2的正三角形,
∴D(2cos30°,2sin30°),即D(![]() ,1),
,1),
∵∠CDB=90°﹣60°=30°,∠BCD=120°
∴∠CDB=30°,即△BCD是等腰三角形,
取BD的中点E,
则BE=1,
则cos30°![]() ,
,
即BC![]() ,即C(
,即C(![]() ,0),
,0),
设E(0,b),0≤b≤2,
则![]() (
(![]() ,b﹣1),
,b﹣1),![]() (
(![]() ,b),
,b),
则![]()
![]() (
(![]() ,b﹣1)(
,b﹣1)(![]() ,b)=2+b(b﹣1)=b2﹣b+2
,b)=2+b(b﹣1)=b2﹣b+2
=(b![]() )2+2
)2+2![]() ═(b
═(b![]() )2
)2![]() ,
,
∴当b![]() 时,数量积取得最小值
时,数量积取得最小值![]() ,
,
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知内角A,B,C所对的边分别为a,b,c,向量m=(2sin B,- ![]() ),n=
),n=![]() ,且m∥n.
,且m∥n.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,且a2+2a4=a9,S6=36.
(1)求an,Sn;
(2)若数列{bn}满足b1=1,![]() ,求证:
,求证:![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com