
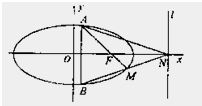
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| m2 |
| 4 |
| n2 |
| 3 |
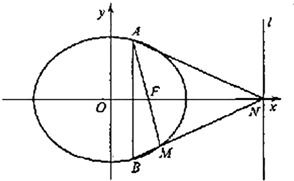 解:
解:| x2 |
| 4 |
| y2 |
| 3 |
| m2 |
| 4 |
| n2 |
| 3 |
| 5m-8 |
| 2m-5 |
| 3n |
| 2m-5 |
| ||
| 4 |
| ||
| 3 |
| (5m-8)2 |
| 4(2m-5)2 |
| 3n2 |
| (2m-5)2 |
| (5m-8)2 |
| 4(2m-5)2 |
| 3n2 |
| (2m-5)2 |
| (5m-8)2+12n2 |
| 4(2m-5)2 |
| (5m-8)2+36-9m2 |
| 4(2m-5)2 |
| x2 |
| 4 |
| y2 |
| 3 |


科目:高中数学 来源: 题型:
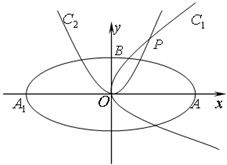 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| 2 |
| 2 |
| 2 |
| QM |
| QN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| a2-1 |
| AP |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| AP |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| m2 |
| y2 |
| n2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com