
【题目】某高中三年级的甲、乙两个同学同时参加某大学的自主招生,在申请的材料中提交了某学科10次的考试成绩,记录如下:
甲:78 86 95 97 88 82 76 89 92 95
乙:73 83 69 82 93 86 79 75 84 99
(1)根据两组数据,作出两人成绩的茎叶图,并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系(不要求计算具体值,直接写出结论即可)
(2)现将两人的名次分为三个等级:
成绩分数 |
|
|
|
等级 | 合格 | 良好 | 优秀 |
根据所给数据,从甲、乙获得“优秀”的成绩组合中随机选取一组,求选中甲同学成绩高于乙同学成绩的组合的概率.
【答案】(1)见解析;(2)![]()
【解析】
(1)以十位为茎,个位数为叶,即可作出茎叶图,由茎叶图的特征即可比较两人的平均成绩以及方差;
(2)用列举法分别列举出从甲、乙均获得“优秀”的成绩组合的基本事件,以及甲同学成绩高于乙同学成绩组合的基本事件,结合古典概型的概率计算公式即可求出结果.
(1)画出甲、乙两人成绩的茎叶图如图:
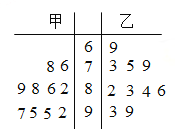
通过茎叶图可以看出,甲成绩的平均值高于乙成绩的平均值,
故甲成绩的方差小于乙成绩的方差。
(2)由表中的数据,甲优秀的数据为:95,97,92,95;
乙优秀的数据为:93,99,
从甲、乙均获得“优秀”的成绩组合的基本事件有:
(95,93),(95,99),(97,93),(97,99),(92,93),(92,99),(95,93),(95,99)共8种不同的取法,
甲同学成绩高于乙同学成绩组合的基本事件是:(95,93),(97,93),(95,93)共3种不同的取法,所以,选中甲同学优秀成绩高于乙同学优秀成绩的组合的概率为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且抛物线
,且抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的一个焦点.
的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() (
(![]() 为坐标原点),求四边形
为坐标原点),求四边形![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,曲线
为奇函数,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,导函数
垂直,导函数![]() 的最小值为-12.
的最小值为-12.
(1)求函数![]() 的解析式;
的解析式;
(2)用列表法求函数![]() 在
在![]() 上的单调增区间、极值、最值.
上的单调增区间、极值、最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)= ,
,
(1)求实数m的值
(2)作出![]() 的图象,并指出当方程
的图象,并指出当方程![]() 只有一解,a的取值范围(不必写过程)
只有一解,a的取值范围(不必写过程)
(3)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是双曲线
分别是双曲线![]() 的左顶点、右焦点,过
的左顶点、右焦点,过![]() 的直线
的直线![]() 与
与![]() 的一条渐近线垂直且与另一条渐近线和
的一条渐近线垂直且与另一条渐近线和![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.若
两点.若![]() ,则
,则![]() 的离心率是( )
的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,已知过点
,已知过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com