
��ֱ������ϵxOy�У�ֱ��l�ķ���Ϊx-y+4=0������C�IJ�������Ϊ 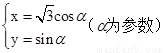 ��
��
������֪�ڼ����꣨��ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x��������Ϊ���ᣩ�У���P�ļ�����Ϊ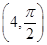 ���жϵ�P��ֱ��l��λ�ù�ϵ��
���жϵ�P��ֱ��l��λ�ù�ϵ��
�������Q������C�ϵ�һ�����㣬������ֱ��l�ľ������ֵ��
���������Ƿ����ֱ��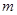 ��
��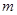 ��l��
��l��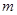 ������C�Ľ���A��B����
������C�Ľ���A��B����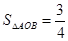 ��
��
������������������������ֱ�߷��̣�����������˵�����ɡ�
����P��0��4������P��ֱ��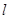 �ϣ�����СֵΪ
�ϣ�����СֵΪ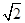 �����ֵΪ
�����ֵΪ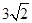 ����
����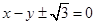 ��
��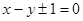
��������
�����������I���Ѽ�����ϵ�µĵ�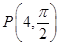 ��Ϊֱ�����꣬��P��0��4��2��
��Ϊֱ�����꣬��P��0��4��2��
��Ϊ��P��ֱ�����꣨0��4������ֱ��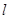 �ķ���
�ķ���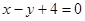 �����Ե�P��ֱ��
�����Ե�P��ֱ��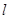 ��.4��
��.4��
��II����Ϊ��Q������C�ϣ��ʿ����Q������Ϊ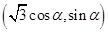 ��5��
��5��
�Ӷ���Q��ֱ��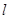 �ľ���Ϊ
�ľ���Ϊ
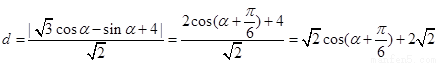 �� 6��
�� 6��
�ɴ˵ã���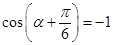 ʱ��dȡ����Сֵ������СֵΪ
ʱ��dȡ����Сֵ������СֵΪ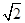
��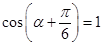 ʱ��dȡ�����ֵ�������ֵΪ
ʱ��dȡ�����ֵ�������ֵΪ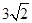 8��
8��
������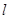 ƽ����m���̣�
ƽ����m���̣�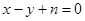 9��
9��
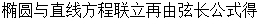
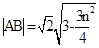
��O��ֱ��m�ľ���Ϊd����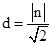 10��
10��

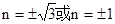 ����֤���������� ������Ϊ
����֤���������� ������Ϊ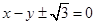 ��
��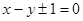 12��
12��
���㣺�����껯ֱ�����꼰ƽ����ֱ������Բ�ཻ�����λ�ù�ϵ
������������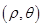 ��ֱ������
��ֱ������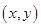 �Ļ���
�Ļ���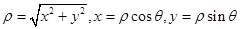 ���ڶ�����������ֵ�����ҵ�����ı���ʽ�����������Ǻ����������н��������ֵ����������ֱ������Բ�ཻ���⣬����������������õ����ҳ������������������ҳ��õ����
���ڶ�����������ֵ�����ҵ�����ı���ʽ�����������Ǻ����������н��������ֵ����������ֱ������Բ�ཻ���⣬����������������õ����ҳ������������������ҳ��õ����


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 3 |
| MN |
| MF1 |
| MF2 |
| OA |
| OB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| OP |
| OQ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ʾ����ֱ������ϵxOy�У�����OA�ڵ�һ���ޣ�����x���������ɶ���60�㣬����P������OA���˶�������Q��y������������˶�����POQ�����Ϊ2
��ͼ��ʾ����ֱ������ϵxOy�У�����OA�ڵ�һ���ޣ�����x���������ɶ���60�㣬����P������OA���˶�������Q��y������������˶�����POQ�����Ϊ2| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com