
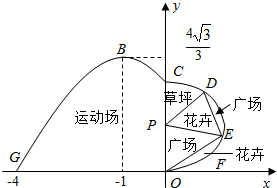
 如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.
如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.
(2)求出休闲区的种植总成本,利用导数确定单调性,即可得出结论.
解答 解:(1)因为最高点B(-1,$\frac{4\sqrt{3}}{3}$),所以A=$\frac{4\sqrt{3}}{3}$,
因为T=$\frac{2π}{ω}$=12,所以ω=$\frac{π}{6}$.
代入点B(-1,$\frac{4\sqrt{3}}{3}$),可得sin(φ-$\frac{π}{6}$)=1,
又0<φ<π,所以φ=$\frac{2π}{3}$,
所以f(x)=$\frac{4\sqrt{3}}{3}$sin($\frac{π}{6}$x+$\frac{2π}{3}$).
(2)由(1)可知点C(0,2),即CO=2,
设种植草坪的每平方米的成本为1,则种植花卉的每平方米的成本是2,
休闲区的种植总成本y=$\frac{θ}{2}$+sinθ+π-2θ-sin2θ=-$\frac{3θ}{2}$+sinθ+π-sin2θ,
∴y′=cosθ-$\frac{3}{2}$-2cos2θ=0,
∴θ=60°,
0°<θ<60°,y′<0,60°<θ<90°,∴θ=60°,函数取得最小值,休闲区的种植总成本最低.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,利用导数研究函数的单调性,根据单调性求函数的最值,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
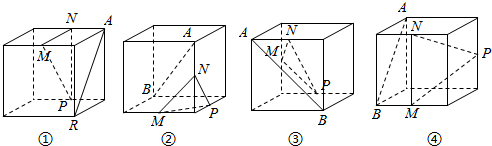
| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
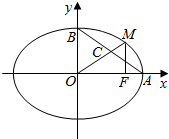 如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期” | |
| B. | “x2+y2=0”是“xy=0”的必要不充分条件 | |
| C. | “若a≤b,则2a≤2b-1”的否命题 | |
| D. | “?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com