
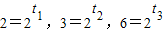 ,
,

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
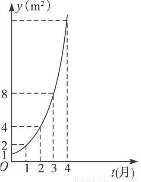
 右图所示的某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系为:y=at.有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过30m2;③浮萍每月增加的面积都相等;④若浮萍蔓延到2m2,3m2,6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.其中判断正确的个数是( )
右图所示的某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系为:y=at.有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过30m2;③浮萍每月增加的面积都相等;④若浮萍蔓延到2m2,3m2,6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.其中判断正确的个数是( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 右图所示的某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系为:y=at.有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过30m2;③浮萍每月增加的面积都相等;④若浮萍蔓延到2m2,3m2,6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.其中判断正确的个数是
右图所示的某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系为:y=at.有以下判断:①这个指数函数的底数为2;②第5个月后,浮萍面积就会超过30m2;③浮萍每月增加的面积都相等;④若浮萍蔓延到2m2,3m2,6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.其中判断正确的个数是查看答案和解析>>
科目:高中数学 来源: 题型:
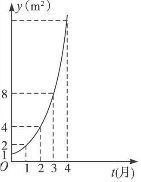
如右图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,有以下叙述:
①这个指数函数的底数为2;②第五个月时,浮萍面积就会超过30 m2;③浮萍从4 m2蔓延至12 m2需要经过1.5个月;④浮萍每月增加的面积都相等;⑤若浮萍蔓延到2 m2,4 m2,8 m2所经过的时间分别为t1,t2,t3,则t1+t2=t3.其中正确的是 ( )
A.①② B.①②③④
C.②③④⑤ D.①②⑤

查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第一次月考文科数学 题型:填空题
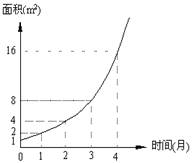
某池塘中野生水葫芦的面积与时间的函数关系的图象,如右图所示. 假设其关系为指数函数,并给出下列说法
①此指数函数的底数为2;
②在第5个月时,野生水葫芦的面积就会超过30m2;
③野生水葫芦从4m2蔓延到12m2只需1.5个月;
④设野生水葫芦蔓延到2m2,3m2, 6m2所需的时间分别为t1, t2, t3, 则有t1 + t2 = t3;
⑤野生水葫芦在第1到第3个月之间蔓延的平均速度等于在第2到第4个月之间蔓延的平均速度.
其中正确的说法有 . (请把正确说法的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com