
 设Rt△ABC中,∠A=90°,AB=1,AC=$\sqrt{3}$,D是线段AC(除端点A、C)上一点,将△ABD沿BD翻折至平面A′BD,使平面A′BD⊥平面ABC,当A′在平面ABC的射影H到平面ABA′的距离最大时,AD的长度为( )
设Rt△ABC中,∠A=90°,AB=1,AC=$\sqrt{3}$,D是线段AC(除端点A、C)上一点,将△ABD沿BD翻折至平面A′BD,使平面A′BD⊥平面ABC,当A′在平面ABC的射影H到平面ABA′的距离最大时,AD的长度为( )| A. | $\root{4}{2}$ | B. | $\root{3}{2}$ | C. | $\root{4}{3}$ | D. | $\root{3}{3}$ |
分析 如图所示,连接A′A.设AD=x,$(0<x<\sqrt{3})$.点H到平面A′AB的距离为h.由于${V}_{{A}^{′}-ABH}$=${V}_{H-{A}^{′}AB}$,可得$\frac{1}{3}×{A}^{′}H$•S△ABH=$\frac{1}{3}$h$•{S}_{△{A}^{′}AB}$,又A′H=$\frac{x}{\sqrt{{x}^{2}+1}}$=AH,S△ABH=$\frac{1}{2}AH•BH$,BH=$\frac{1}{\sqrt{{x}^{2}+1}}$.A′A=$\sqrt{2}AH$,${S}_{△AB{A}^{′}}$=$\frac{1}{2}{A}^{′}A$•$\sqrt{1-\frac{1}{4}({A}^{′}A)^{2}}$,代入化简利用基本不等式的性质即可得出.
解答  解:如图所示,连接A′A.
解:如图所示,连接A′A.
设AD=x,$(0<x<\sqrt{3})$.点H到平面A′AB的距离为h.
∵${V}_{{A}^{′}-ABH}$=${V}_{H-{A}^{′}AB}$,
$\frac{1}{3}×{A}^{′}H$•S△ABH=$\frac{1}{3}$h$•{S}_{△{A}^{′}AB}$,
又A′H=$\frac{x}{\sqrt{{x}^{2}+1}}$=AH,S△ABH=$\frac{1}{2}AH•BH$,BH=$\frac{1}{\sqrt{{x}^{2}+1}}$.
A′A=$\sqrt{2}AH$,${S}_{△AB{A}^{′}}$=$\frac{1}{2}{A}^{′}A$•$\sqrt{1-\frac{1}{4}({A}^{′}A)^{2}}$,
h=$\frac{{A}^{′}H•BH}{\sqrt{2}×\sqrt{1-\frac{1}{2}A{H}^{2}}}$=$\frac{\frac{x}{\sqrt{{x}^{2}+1}}×\frac{1}{\sqrt{{x}^{2}+1}}}{\sqrt{2-\frac{{x}^{2}}{{x}^{2}+1}}}$=$\frac{x}{\sqrt{{x}^{4}+3{x}^{2}+2}}$=$\frac{1}{\sqrt{{x}^{2}+\frac{2}{{x}^{2}}+3}}$≤$\frac{1}{\sqrt{2\sqrt{2}+3}}$,当且仅当x=$\root{4}{2}$时取等号.
∴当A′在平面ABC的射影H到平面ABA′的距离最大时,AD的长度为$\root{4}{2}$.
故选:A.
点评 本题考查了空间线面位置关系、三棱锥体积计算公式、勾股定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:选择题
在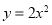 上有一点
上有一点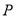 ,它到
,它到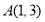 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点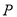 的坐标是( )
的坐标是( )
A.(-2,1) B.(1,2) C.(2,1) D.(-1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
圆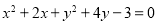 上到直线
上到直线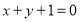 的距离为
的距离为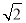 的点共有( )
的点共有( )
A.1个 B.2个 C. 3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
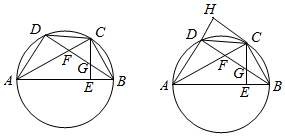 如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,
如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
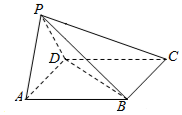 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD是平行四边形,∠ADC=120°,AB=2AD.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD是平行四边形,∠ADC=120°,AB=2AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com