
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围.
的取值范围.
(![]() )若
)若![]() 关于的方程
关于的方程![]() 有区间
有区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(相等的实数根算一个).
的取值范围(相等的实数根算一个).
【答案】(1)![]() .
.
(2)![]() .
.
(3)![]() .
.
【解析】试题分析:(1)只要设![]() ,代入已知条件即可求得
,代入已知条件即可求得![]() ;(2)由(1)知
;(2)由(1)知![]() 是二次函数,其单调性与对称轴有关,题意说明其对称轴不在区间
是二次函数,其单调性与对称轴有关,题意说明其对称轴不在区间![]() 上;(3)关于
上;(3)关于![]() 的方程
的方程![]() 是二次方程
是二次方程![]() ,它在区间
,它在区间![]() 上有唯一实数根,可能是在
上有唯一实数根,可能是在![]() 上是两个相等的实根,也可能是一根在此区间上,另一根在此区间外(注意区间端点的讨论).
上是两个相等的实根,也可能是一根在此区间上,另一根在此区间外(注意区间端点的讨论).
试题解析:(1)设![]() ,代入
,代入![]() ,
,
得![]() ,对于
,对于![]() 恒成立,故
恒成立,故![]() ,
,
又由![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴![]() .
.
(2)因为![]()
![]() ,
,
又函数![]() 在
在![]() 上是单调函数,故
上是单调函数,故![]() 或
或![]() ,
,
截得![]() 或
或![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .
.
(3)由方程![]() 得
得![]() ,
,
令![]() ,
,![]() ,
,
即要求函数![]() 在
在![]() 上有唯一的零点,
上有唯一的零点,
①![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() 或3,不合题意;
或3,不合题意;
②若![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() 或2,满足提议,故
或2,满足提议,故![]() 成立;
成立;
③若△![]() ,则
,则![]() ,代入原方程得
,代入原方程得![]() ,满足提议,故
,满足提议,故![]() 成立;
成立;
④若![]() 且
且![]() 且
且![]() 时,由
时,由![]() 得
得![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天时间与水深(单位:米)的关系表:
时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
水深 | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)请用一个函数来近似描述这个港口的水深y与时间t的函数关系;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上认为是安全的(船舶停靠时,船底只要不碰海底即可)。某船吃水深度(船底离地面的距离)为6.5米。
Ⅰ)如果该船是旅游船,1:00进港希望在同一天内安全出港,它至多能在港内停留多长时间(忽略进出港所需时间)?
Ⅱ)如果该船是货船,在2:00开始卸货,吃水深度以每小时0.5米的速度减少,由于台风等天气原因该船必须在10:00之前离开该港口,为了使卸下的货物尽可能多而且能安全驶离该港口,那么该船在什么整点时刻必须停止卸货(忽略出港所需时间)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为
,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为 ![]()
(1)求椭圆C的方程;
(2)设过点B且斜率为k的动直线l与椭圆C的另一个交点为M, ![]() =λ(
=λ( ![]() ),若点N在圆O上,求正实数λ的取值范围.
),若点N在圆O上,求正实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.
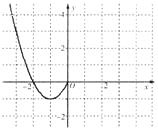
(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民中学为了了解该校高一年级学生的数学成绩,从高一年级期中考试成绩中抽出100名学生的成绩,由成绩得到如下的频率分布直方图.

根据以上频率分布直方图,回答下列问题:
(1)求这100名学生成绩的及格率;(大于等于60分为及格)
(2)试比较这100名学生的平均成绩和中位数的大小.(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,函数
时,函数![]() 与
与![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值;
的值;
(2)若函数![]() 在定义域内不单调,求
在定义域内不单调,求![]() 的取值范围;
的取值范围;
(3)是否存在正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,∠BAC=90°,AB= AC = AA1=2,M,N分别是A1B1,BC的中点.
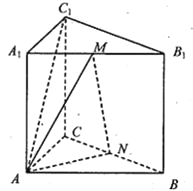
(1)证明:MN∥平面ACC1A1;
(2)求二面角M﹣AN﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com