
【题目】已知椭圆G:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于点C,且点C在线段AB上.
,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于点C,且点C在线段AB上.
(1)求椭圆G的方程;
(2)若|AF1|=|CB|,求直线l的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
⑴设椭圆焦距为2c运用离心率公式和![]() 的关系,即可得到椭圆方程
的关系,即可得到椭圆方程
⑵由题意可知直线![]() 斜率存在,可设直线
斜率存在,可设直线![]() ,代入椭圆方程,运用韦达定理和向量共线的坐标表示,解方程即可得到所求方程
,代入椭圆方程,运用韦达定理和向量共线的坐标表示,解方程即可得到所求方程
(1)设椭圆焦距为2c,由已知可得![]() ,且c=1,
,且c=1,
所以a=2,即有b2=a2-c2=3,
则椭圆G的方程为![]() =1.
=1.
(2)由题意可知直线l斜率存在,可设直线l:y=k(x+1),由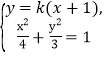 消y,
消y,
并化简整理得(4k2+3)x2+8k2x+4k2-12=0.
由题意可知Δ>0,
设A(x1,y1),B(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因为点C,F1都在线段AB上,且|AF1|=|CB|,
所以![]() ,即(-1-x1,-y1)=(x2,y2-yC),
,即(-1-x1,-y1)=(x2,y2-yC),
所以-1-x1=x2,即x1+x2=-1,
所以x1+x2=![]() =-1,
=-1,
解得k2=![]() ,即k=±
,即k=±![]() .
.
所以直线l的方程为y=![]() (x+1)或y=-
(x+1)或y=-![]() (x+1).
(x+1).


科目:高中数学 来源: 题型:
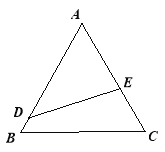
【题目】如图所示,公园内有一块边长为![]() 的等边
的等边![]() 形状的三角地,现修成草坪,图中
形状的三角地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.
(Ⅰ)设![]()
![]() ,试用
,试用![]() 表示
表示![]() 的函数关系式;
的函数关系式;
(Ⅱ)如果![]() 是灌溉水管,为节约成本希望它最短,
是灌溉水管,为节约成本希望它最短,![]() 的位置应该在哪里?如果
的位置应该在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长,![]() 的位置又在哪里?请给予证明.
的位置又在哪里?请给予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面PDC,E为棱PD的中点.
(1)求证:PB∥平面EAC;
(2)求证:平面PAD⊥平面ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°,相距20海里的C处的乙船,现乙船朝北偏东![]() 的方向即沿直线CB前往B处救援,则
的方向即沿直线CB前往B处救援,则![]() 等于 ( )
等于 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{cn}的前n项和为Tn , 若数列{cn}满足各项均为正项,并且以(cn , Tn)(n∈N*)为坐标的点都在曲线 ![]() 上运动,则称数列{cn}为“抛物数列”.已知数列{bn}为“抛物数列”,则( )
上运动,则称数列{cn}为“抛物数列”.已知数列{bn}为“抛物数列”,则( )
A.{bn}一定为等比数列
B.{bn}一定为等差数列
C.{bn}只从第二项起为等比数列
D.{bn}只从第二项起为等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,点(0,
,点(0,![]() )是椭圆与y轴的一个交点.
)是椭圆与y轴的一个交点.

(1)求椭圆C的方程;
(2)直线x=2与椭圆交于P,Q两点,点P位于第一象限,A,B是椭圆上位于直线x=2两侧的动点;
①若直线AB的斜率为![]() ,求四边形APBQ面积的取值范围;
,求四边形APBQ面积的取值范围;
②当点A,B在椭圆上运动,且满足∠APQ=∠BPQ时,直线AB的斜率是否为定值?若是,求出此定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2014年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2008年至2014年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.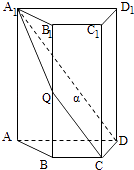
(1)证明:Q为BB1的中点;
(2)若AA1=4,CD=2,梯形ABCD的面积为6,∠ADC=60°,求平面α与底面ABCD所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱台ABCD﹣A1B1C1D1中,平面BCC1B1⊥平面ABCD,四边形ABCD为平行四边形,四边形BCC1B1为等腰梯形,BC=4,B1C1=C1C=2,AB=5,AC⊥BC. 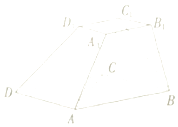
(1)求证:BC1⊥平面ACC1;
(2)求直线BC1与平面ADD1A1所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com