
(19) (本小题满分12分)(注决:在试题卷上作答无效)
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,
,
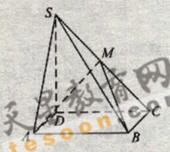
![]() ,
,![]() ,点
,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 。
。
![]() 证明:
证明:![]() 是侧棱
是侧棱![]() 的中点;
的中点;
![]() 求二面角
求二面角![]() 的大小。
的大小。
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
. 19(本小题满分14分)
 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线
x+y-1 = 0相交于A、B两点,且OA⊥OB
(O为坐标原点).
(I) 求 + 的值;
(II) 若椭圆长轴长的取值范围是[,],
求椭圆离心率e的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三质量检测理科数学 题型:解答题
(本小题满分1 3分)
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
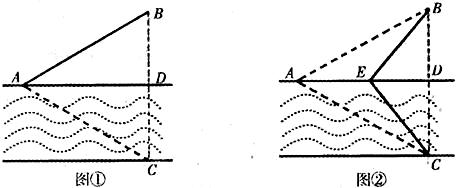
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤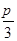 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测理科数学 题型:解答题
(本小题满分1
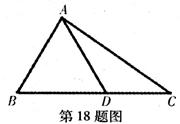
3分)如图,在△ABC中,已知B=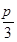 ,AC=4
,AC=4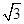 ,D为BC边上一点.
,D为BC边上一点.
(I)若AD=2,S△ABC=2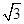 ,求DC的长;
,求DC的长;
(Ⅱ)若AB=AD,试求△ADC的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2010湖北理数)19(本小题满分12分)
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有![]() ?若存在,求出m的取值范围;若不存在,请说明理由。
?若存在,求出m的取值范围;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com