
【题目】如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=
∠ACD=90°,∠EAC=60°,AB=AC=AE.
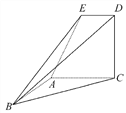
(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论.
(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(Ⅰ)由题意及图形取AB的中点F,AC的中点M,得到四边形EMCD为矩形,利用线面平行的判定定理证得线面平行;
(Ⅱ)由题意利用二面角的定义得到二面角的平面角,然后在三角形中解出即可.
试题解析:
(1)线段BC的中点就是满足条件的点P.
证明如下:
取AB的中点F,连接DP,PF,EF,
则FP∥AC,FP=![]() AC,
AC,
取AC的中点M,连接EM,EC,
因为AE=AC且∠EAC=60°,
所以△EAC是正三角形,所以EM⊥AC.
所以四边形EMCD为矩形,
所以ED=MC=![]() AC.
AC.
又因为ED∥AC,
所以ED∥FP且ED=FP,
所以四边形EFPD是平行四边形,所以DP∥EF,
而EF平面EAB,DP平面EAB,
所以DP∥平面EAB.
(2)过C作CG∥AB,过B作BG∥AC,CG∩BG=G,连接GD.
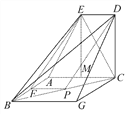
因为ED∥AC,所以ED∥BG,
所以B,E,D,G四点共面,
所以平面EBD与平面ABC相交于BG,
因为CD⊥AC,平面ACDE⊥平面ABGC,
所以CD⊥平面ABGC,
又因为BG平面ABGC,
所以BG⊥CD,
又BG⊥GC,CD∩GC=C,
所以BG⊥平面CDG,
所以BG⊥DG,
所以∠DGC是平面EBD与平面ABC所成的锐二面角θ,设AB=AC=AE=a,
则GC=AB=a,DC=EM=![]() a,
a,
所以GD=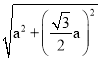 =
=![]() a,
a,
所以cosθ=cos∠DGC=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某产品出厂前需要依次通过三道严格的审核程序,三道审核程序通过的概率依次为 ![]() ,
, ![]() ,
, ![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,该产品只有三道程序都通过才能出厂销售 (Ⅰ)求审核过程中只通过两道程序的概率;
,每道程序是相互独立的,且一旦审核不通过就停止审核,该产品只有三道程序都通过才能出厂销售 (Ⅰ)求审核过程中只通过两道程序的概率;
(Ⅱ)现有3件该产品进入审核,记这3件产品可以出厂销售的件数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 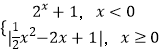 ,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
A.[6,11]
B.[3,11]
C.(6,11)
D.(3,11)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax2 , a>0.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x满足|x﹣3|≤1.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 点P(x0 ,
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 点P(x0 , ![]() )为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为
)为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为 ![]() ,则双曲线的离心率是 .
,则双曲线的离心率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com