
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(![]() )若圆心
)若圆心![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,求切线的方程.
的切线,求切线的方程.
(![]() )若圆
)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() 或
或![]() ;(
;(![]() )
)![]() .
.
【解析】试题分析:(1)根据圆心与半径得到圆![]() 的方程,设出切线方程为
的方程,设出切线方程为![]() ,利用圆心到切线的距离1,解出
,利用圆心到切线的距离1,解出![]() 的值即可得切线方程;(2)设
的值即可得切线方程;(2)设![]() ,由
,由![]() ,利用两点间的距离公式列出关系式,整理后得到点
,利用两点间的距离公式列出关系式,整理后得到点![]() 的轨迹为以
的轨迹为以![]() 为圆心,2为半径的圆,可记为圆
为圆心,2为半径的圆,可记为圆![]() ,由
,由![]() 在圆
在圆![]() 上,得到圆
上,得到圆![]() 与圆
与圆![]() 相交或相切,根据两圆的半径长,得出两圆心间的距离范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到
相交或相切,根据两圆的半径长,得出两圆心间的距离范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到![]() 的范围.
的范围.
试题解析:(![]() )圆心的坐标
)圆心的坐标![]() ,半径为
,半径为![]() ,圆的方程:
,圆的方程: ![]() ,
,
又设切线的方程为![]() ,
,
∴切线到圆心的距离![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 或
或![]() ,∴
,∴![]() 或
或![]() ,即为
,即为![]() 或
或![]() ,
,
切线的方程为![]() 或
或![]() .
.
(![]() )设点
)设点![]() ,由
,由![]() ,知:
,知: ![]() ,化简得:
,化简得: ![]() ,
,
∴点![]() 的轨迹方程以
的轨迹方程以![]() 为圆心,半径为
为圆心,半径为![]() 的圆,记为圆
的圆,记为圆![]() ,
,
∵点![]() 在圆
在圆![]() 上,∴圆
上,∴圆![]() 与圆
与圆![]() 的关系为相切或相交,
的关系为相切或相交,
∴![]() ,∴
,∴![]() ,∴解不等式:
,∴解不等式: ![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中
的组合体中![]() ,
,![]() . 台体体积公式:
. 台体体积公式: ![]() , 其中
, 其中![]() 分别为台体上、下底面面积,
分别为台体上、下底面面积, ![]() 为台体高.
为台体高.
(1)证明:直线![]()
![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
, ![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求 该组合体的体积.
,求 该组合体的体积. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:
满足:
①对于任意的![]() ,都有
,都有![]() ;
;
②当![]() 时,
时,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值,并判断函数
的值,并判断函数![]() 的奇偶性;
的奇偶性;
(2)判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(3)求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
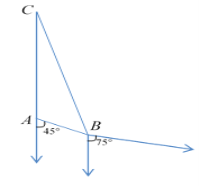
【题目】如图,在海岸A处,发现南偏东45°方向距A为(2![]() -2)海里的B处有一艘走私船,在A处正北方向,距A为
-2)海里的B处有一艘走私船,在A处正北方向,距A为![]() 海里的C处的缉私船立即奉命以10
海里的C处的缉私船立即奉命以10![]() 海里/时的速度追截走私船.
海里/时的速度追截走私船.
(1)刚发现走私船时,求两船的距离;
(2)若走私船正以10![]() 海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:
海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:![]() ≈1.4,
≈1.4,![]() ≈2.5).
≈2.5).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1 , 直线C2的极坐标方程分别为ρ=4sinθ,ρcos( ![]() )=2
)=2 ![]() .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为  (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求四棱锥![]() 的体积;
的体积;
(2)求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() 四点共面? (结论不要求证明)
四点共面? (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]()
![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,问:以线段
,问:以线段![]() 为直径的圆是否经过一定点
为直径的圆是否经过一定点![]() ?若存在,求出定点
?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过点
的图像经过点![]() ,且满足
,且满足![]() ,
,
(1)求![]() 的解析式;
的解析式;
(2)已知![]() ,求函数
,求函数![]() 在
在![]() 的最大值和最小值;
的最大值和最小值;
函数![]() 的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由
的图像上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com