
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为![]() (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)(x-3)2+(y-1)2=4,(2)![]()
【解析】
(1)先根据![]() 将曲线C1的极坐标方程化为直角坐标方程,再根据中点坐标公式得用Q坐标表示P,代入点P满足得曲线C1直角坐标方程,即得点Q的轨迹C2的直角坐标方程;(2)根据垂径定理得圆心(3,1)到直线的距离不大于1,再消参数得直线l的直角坐标方程,最后利用点到直线距离公式化简不等式,解出实数a的取值范围.
将曲线C1的极坐标方程化为直角坐标方程,再根据中点坐标公式得用Q坐标表示P,代入点P满足得曲线C1直角坐标方程,即得点Q的轨迹C2的直角坐标方程;(2)根据垂径定理得圆心(3,1)到直线的距离不大于1,再消参数得直线l的直角坐标方程,最后利用点到直线距离公式化简不等式,解出实数a的取值范围.
(1)根据题意得,
曲线C1的直角坐标方程为x2+y2-4y=12,
设点P(x′,y′),Q(x,y),
根据中点坐标公式,得
![]() 代入x2+y2-4y=12,
代入x2+y2-4y=12,
得点Q的轨迹C2的直角坐标方程为(x-3)2+(y-1)2=4,
(2)直线l的直角坐标方程为y=ax,根据题意,得圆心(3,1)到直线的距离d≤![]() =1,即
=1,即![]() ≤1,
≤1,
解得0≤a≤![]() .
.
∴实数a的取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).

规定:当食品中的有害微量元素的含量在![]() 时为一等品,在
时为一等品,在![]() 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是空气质量的一个重要指标,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35μg/m3以下空气质量为一级,在35μg/m3~75μg/m3之间空气质量为二级,在75μg/m3以上空气质量为超标.如图是某市2019年12月1日到10日PM2.5日均值(单位:μg/m3)的统计数据,则下列叙述不正确的是( )
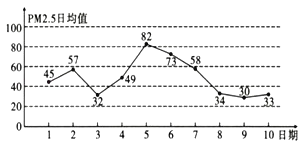
A.这10天中,12月5日的空气质量超标
B.这10天中有5天空气质量为二级
C.从5日到10日,PM2.5日均值逐渐降低
D.这10天的PM2.5日均值的中位数是47
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由具有公共直角边的两块直角三角板(
是由具有公共直角边的两块直角三角板(![]() 与
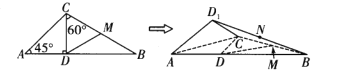
与![]() )组成的三角形,如左下图所示.其中,
)组成的三角形,如左下图所示.其中,![]() .现将
.现将![]() 沿斜边
沿斜边![]() 进行翻折成
进行翻折成![]() (
(![]() 不在平面
不在平面![]() 上).若
上).若![]() 分别为
分别为![]() 和
和![]() 的中点,则在
的中点,则在![]() 翻折过程中,下列命题不正确的是( )
翻折过程中,下列命题不正确的是( )
A. 在线段![]() 上存在一定点
上存在一定点![]() ,使得
,使得![]() 的长度是定值
的长度是定值
B. 点![]() 在某个球面上运动
在某个球面上运动
C. 存在某个位置,使得直线![]() 与
与![]() 所成角为
所成角为![]()
D. 对于任意位置,二面角![]() 始终大于二面角
始终大于二面角![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自湖北爆发新型冠状病毒肺炎疫情以来,湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送240t物资.已知每辆卡车每天往返的次数为A型卡车5次,B型卡车4次,每辆卡车每天往返的成本A型卡车1200元,B型卡车1800元,则每天派出运输队所花的成本最低为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.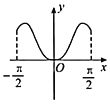
C.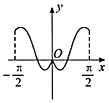 D.
D.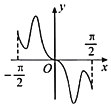
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com