
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $-\frac{{4\sqrt{3}}}{3}$ |
分析 根据不等式x2-4ax+3a2<0(a<0)的解集为(x1,x2),利用韦达定理求出${x}_{1}{x}_{2}=3{a}^{2}$,x1+x2=4a,带入利用基本不等式的性质求解.
解答 解:不等式x2-4ax+3a2<0(a<0)的解集为(x1,x2),
根据韦达定理,可得:${x}_{1}{x}_{2}=3{a}^{2}$,x1+x2=4a,
那么:${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$=4a+$\frac{1}{3a}$.
∵a<0,
∴-(4a+$\frac{1}{3a}$)≥2$\sqrt{4a×\frac{1}{3a}}$=$\frac{4\sqrt{3}}{3}$,即4a+$\frac{1}{3a}$≤-$\frac{4\sqrt{3}}{3}$
故${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最大值为$-\frac{4\sqrt{3}}{3}$.
故选:D.
点评 本题主要考查了一元二次不等式的应用,以及根与系数的关系,同时考查了基本不等式的性质的运用的能力和计算能力,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
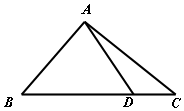 如图,已知D是△ABC边BC上一点.
如图,已知D是△ABC边BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
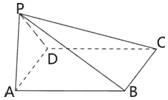 如图,平面PAD⊥平面ABCD,ABCD是边长为2的菱形,PA=PD,且∠APD=90°,∠DAB=60°.
如图,平面PAD⊥平面ABCD,ABCD是边长为2的菱形,PA=PD,且∠APD=90°,∠DAB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
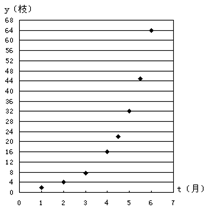 如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )| A. | 二次函数:y=2t2 | B. | 幂函数:y=t3 | ||
| C. | 指数函数:y=2t | D. | 对数函数:y=log2t |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com