
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是( )
,下列选项中,不可能成立的是( )
A. ![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素 B.
有一个最小元素 B. ![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C. ![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素 D.
有一个最小元素 D. ![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系![]() 中,
中,![]() 点
点![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() 的方程为
的方程为![]()
B. 在![]() 轴上存在异于
轴上存在异于![]() 的两定点
的两定点![]() ,使得
,使得![]()
C. 当![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D. 在![]() 上存在点
上存在点![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
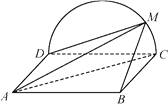
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足① ![]() ;② 当
;② 当![]() ,且
,且![]() 时,都有
时,都有![]() ;③ 当
;③ 当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:①
为“偏对称函数”.现给出四个函数:①![]() ;②
;② ![]() ; ③
; ③![]() ;④
;④![]() .则其中是“偏对称函数”的函数序号为 _______.
.则其中是“偏对称函数”的函数序号为 _______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
①甲地该月11时的平均气温低于乙地该月11时的平均气温
②甲地该月11时的平均气温高于乙地该月11时的平均气温
③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差
④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差
其中根据茎叶图能得到的正确结论的编号为( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有![]() 、
、![]() 两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
两个岗位招聘大学毕业生,其中第一天收到这两个岗位投简历的大学生人数如下表:
|
| 总计 | |
女生 | 12 | 8 | 20 |
男生 | 24 | 56 | 80 |
总计 | 36 | 64 | 100 |
(1)根据以上数据判断是有![]() 的把握认为招聘的
的把握认为招聘的![]() 、
、![]() 两个岗位与性别有关?
两个岗位与性别有关?
(2)从投简历的女生中随机抽取两人,记其中投![]() 岗位的人数为
岗位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),……,第八组[190.195],下图是按上述分组方法得到的频率分布直方图.
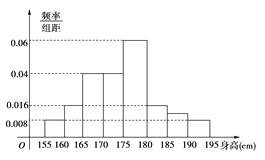
(1)求第七组的频数;
(2)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com