练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    椭圆+=1上有不同的三点A(x,y)，B(4,)，C(x,y)，它们与焦点F(4,0)的距离成等差数列.  (1)求x+x的值；(2)求证线段AC的垂直平分线过定点.

    （1）a-ex1+a-ex2=2 (a-4e)

              -e (x1+x2)=-8e

              ∴x1+x2=8

         （2）AC中垂线：y-(x-4)

              ∵9x12+25y12=225

                9x12+25y22=225

              ∴9(x1-x2) (x1+x2)+25 (y1-y­2­) (y1+y2)=0

              ∴=(y1+y2)

              ∴：y-(y1+y2) (x-4)

                    y-

                 过y=0

                 1+   交点（，0）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆方程为
    x2
    4
    +
    y2
    3
    =1    ，试确定m的范围，使得椭圆上有不同的两点关于直线y=4x+m对称．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    椭圆+=1上有n个不同的点P1、P2、P3、…、Pn,F是右焦点,|P1F|,|P2F|,…,|PnF|组成公差d＞的等差数列,则n的最大值是(    )

    A.199              B.200               C.99               D.100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的方程为+=1,试确定m的取值范围，使得对一直线y=4x+m,椭圆C上有不同两点P、Q关于该直线对称.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省南昌市高三第二次模拟测试理科数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    (1)已知等差数列{an}的前n项和为Sn，若m+n=s+t(m,n,s,t∈N*，且m≠n,s≠t)，证明；= ；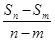

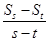    (2)注意到(1)中Sn与n的函数关系，我们得到命题：设抛物线x2=2py(p>0)的图像上有不同的四点A，B，C，D，若xA，xB，xC，xD分别是这四点的横坐标，且xA+xB=xC+xD，则AB∥CD，判定这个命题的真假，并证明你的结论

    (3)我们知道椭圆和抛物线都是圆锥曲线，根据(2)中的结论，对椭圆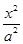+ =1(a>b>0)提出一个有深度的结论，并证明之.

     

    查看答案和解析>>

    同步练习册答案