
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 有两个相异零点
有两个相异零点![]() ,
, ![]() ,求证:
,求证: ![]() .(其中e为自然对数的底数)
.(其中e为自然对数的底数)
【答案】(Ⅰ)见解析; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由题意得![]() ,分
,分![]() 和
和![]() 两种情况分类讨论,即可求解函数的单调区间;
两种情况分类讨论,即可求解函数的单调区间;
(Ⅱ)要证: ![]() ,即证
,即证![]() ,不妨设
,不妨设![]() ,∵
,∵![]() ,
, ![]() 是函数
是函数![]() 的零点, 化简
的零点, 化简![]() ,则转化为证:
,则转化为证: ![]() ,构造函数
,构造函数![]() ,利用
,利用![]() 单调性与最值,即可作出证明.
单调性与最值,即可作出证明.
试题解析:(Ⅰ) ![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
① 当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增,
上单调递增,
② 当![]() 时,令
时,令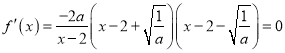 ,解得
,解得![]() ,
,
![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增,
单调递增,
![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递减,
单调递减,
综上所述,当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() 在
在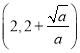 上单调递增,在
上单调递增,在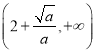 上单调递减;
上单调递减;
(Ⅱ)证法一 要证: ![]() ,则证
,则证![]() ,
,
即证![]() ,
,
不妨设![]() ,∵
,∵![]() ,
, ![]() 是函数
是函数![]() 的零点,则
的零点,则![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
则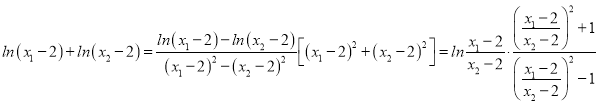 ,
,
则转化为证: ,令
,令![]() ,则
,则![]() ,
,
于是即证: ![]() ,可化为
,可化为![]() ,即证
,即证![]() ,
,
构造函数![]() ,
, ![]() ,
,
令![]() ,则
,则![]() ,则
,则![]() 在
在![]() 单增,则
单增,则![]() ,
,
则![]() ,则
,则![]() 在
在![]() 单增,则
单增,则![]() ,即
,即![]() 成立,
成立,
所以![]() 成立.
成立.
证法二 ![]() 的定义域为
的定义域为![]() ,要证:
,要证: ![]() ,则证
,则证![]() ,
,
即证![]() ,令
,令![]() ,
, ![]() ,
,
即证![]() ,也即证
,也即证![]() ,
,
因为![]() ,
, ![]() 是函数
是函数![]() 的相异零点,则
的相异零点,则![]() ,
, ![]() ,
,
所以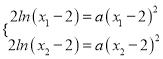 ,即
,即![]() ,所以,
,所以, 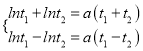 ,
,
所以 ,
,
不妨设![]() ,则
,则![]() ,令
,令![]() (
(![]() ),
),
要证![]() ,则转化为证
,则转化为证![]() (其中
(其中![]() ),即证
),即证![]() ,……10分
,……10分
令![]() (
(![]() ),则
),则![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即
,即![]() 成立,
成立,
从而原命题![]() 成立
成立
证法三 ![]() 的定义域为
的定义域为![]() ,要证:
,要证: ![]() ,则证
,则证![]() ,
,
即证![]() ,令
,令![]() ,
, ![]() ,
, ![]() ,
,
则转化为证明命题“函数![]() 有两个相异的零点
有两个相异的零点![]() ,
, ![]() ,求证
,求证![]() ”,……6分
”,……6分
∵![]() ,
,
①当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() 没有两个零点,不合题意;
没有两个零点,不合题意;
②当![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
要使![]() 有两个相异零点,则
有两个相异零点,则![]() ,解得
,解得![]() ;
;
且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
不妨设![]() ,要证
,要证![]() ,即证
,即证![]() ,
,
而![]() ,所以
,所以![]() ,
, ![]() ,
,
而函数![]() 在
在![]() 上单调递增,要证
上单调递增,要证![]() ,只要证
,只要证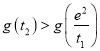 ,而
,而![]() ,即证
,即证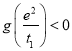 ,
,
由于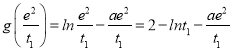 ,而
,而![]() ,即
,即![]() ,
,
∴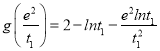 (
(![]() ),记
),记![]() (
(![]() ),
),
∴![]() ,
,
令![]() (
(![]() ),则
),则![]() ,
,
∴![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,即
,即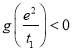 成立,
成立,
从而原命题![]() 成立 .
成立 .


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷![]() 份,
份, ![]() 名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
(1)要从这![]() 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取![]() 名中小学生进一步调查,则在
名中小学生进一步调查,则在![]() (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?
(2)若希望![]() 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于![]() (小时),请估计
(小时),请估计![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
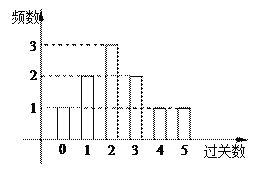
【题目】某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过![]() 关者奖励
关者奖励![]() 件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
件小奖品(奖品都一样).下图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
(Ⅰ)求小明在这十次游戏中所得奖品数的均值;
(Ⅱ)规定过三关者才能玩另一个高级别的游戏,估计小明一次游戏后能玩另一个游戏的概率;
(Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4},小聪在某四次游戏中所过关数为{3,3,4,5},现从中各选一次游戏,求小明和小聪所得奖品总数超过10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,已知直线l1:
中,已知直线l1: ![]() (
(![]() ,
, ![]() ),抛物线C:
),抛物线C:  (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() , 得到如图所示的几何体.
, 得到如图所示的几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com